東大志望の受験生のためのサイト

第13回　出典：東京大学前期　2011年　理系数学　第3問

　皆さん、こんにちは。特に受験生の方はセンター試験お疲れ様でした！　2次試験が目前に見えてきていよいよという感じでしょうが、受験生にとってのここからの成長って本当に大きいんです。最後まで気を抜かずに頑張ってください！


　2015年度入試から始まる新課程では、新たに“曲線の長さ”が数学Ⅲの範囲になります。これまでの課程で次の“曲線の長さ（弧長）を求める公式”を明確に入試の出題範囲としている大学は京都大学くらいのものでしたが、数学が得意だったり進学校に通っていたりする人の中には知っている方も少なくないでしょう。

　媒介変数 t について微分可能な2つの関数 x(t),y(t) によって

　　　

とパラメータ表示される曲線の長さ s は、

と表せる.

　どうしてこうなるのかについて、A級紙第4回から散々取り扱ってきた積分の考え方がしっくりきている人には、次のイメージが十分伝わるかと思います。

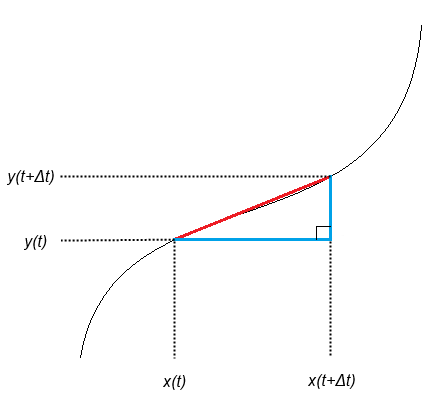
　媒介変数 t → t+Δt に対応する曲線上の2点を結ぶ、図の赤線部の長さ Δs は、三平方の定理から

　　

　ここで Δt → 0 の極限を取れば赤線の長さは微小となり、ほぼ2点間を結ぶ曲線の長さに等しいと見なせるようになるから、t=a から t=b まで t を連続的に変化させて Δs を足し合わせたものが s であると考えれば、上の公式を得る.

　さて、これを踏まえて東大理系2011年第3問(2)を見れば、計算すべき積分値 f(a) が何らかの弧長を表していることは一目瞭然。とすれば、(3)で計算する極限に何らかの視覚的意味を見出したくなるのは人の性（？）ですね。

　題意の点Q が媒介変数 t を変化させたときに描く軌跡を“双曲螺旋”と言って、このグラフ自体は普通極座標で

などと表されます（点Qの軌跡では θ → L/t、b=L とすればよい）。大学入試で別段重要な曲線という訳でもありませんが、概形はこんな感じ。

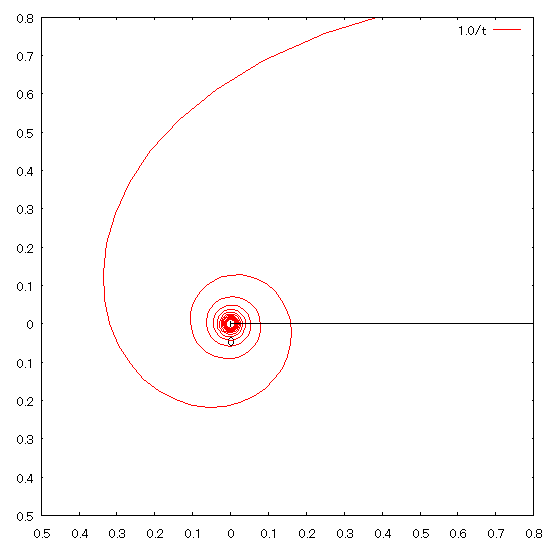
▲双曲螺旋

※b=1.0、θ＞0として作図

　ちなみに受験直前期ならこの軌跡の無限遠での様子を計算できてほしいところですが、いかがです？

⇒答え


　話を戻して、(3)の について考えましょう。落ち着いて条件を整理すると、f(a) は『 t を a≦t≦1 の範囲で動かした時の点Qの軌跡（双曲螺旋の一部）の弧長』のことでした。 t=1 に対応するのはどこかの点であって、t →+0 とすると点Qは原点に限りなく近づくことになるのが分かりますから、上図を見ればQが原点の周りをぐるぐる回って弧長 f(a) がどんどん長くなっていくのは明らか。対する log a は -∞ に発散しますから、題意の極限が何らかの負の定数値に収束してもおかしくなさそうです。

　結局感覚的な理解はここまでで、答えを知るにはやっぱり計算するしかないのですが、何らかの図形的解釈ができる計算に対し状況をイメージすることは基本的には大切にしたい精神です。勿論試験中にここまでやることは要求しませんが、解き終わった後の問題についてぼーっと理解を深めるのもまた良い勉強。実際、サイクロイドが円を転がした時に出てくる軌跡だというのはいろんな参考書に書いてありますが、軌跡としての双曲螺旋が図形的に本問のようにして描かれるというのはなかなかお目にかからない事実でしょう。
　高校数学の『いろいろな曲線』では、教科書にオマケ程度の扱いでも様々な曲線が紹介されていますよね。東大受験に際してこれらの曲線の名前とその性質を覚えておく必要は殆ど無いでしょうが、せめて出てきたときくらいは、特殊な図形的性質を持つ曲線が比較的シンプルな式で表されてしまう面白さを感じることのできる、“とりあえず見てみよう”というその気持ち、無垢な心を忘れたくないものです。だって東大が本問を本当にただの計算問題として出題したかったのなら、回りくどい問題設定も(1)も必要なかったはずなんですから。それではまた次回。

2014/01/24 石橋雄毅