分野別過去問解説です。今回は複素数平面に関する問題を二問。一問はとても綺麗に解ける良問を,もう一問は旧課程の“一次変換”としての出題だったものの,複素数平面を用いても解ける問題を解説します。
問題1
まずは2016年理系第1問。
$z$ を複素数とする。複素数平面上の3点 A($1$), B($z$), C($z^2$) が鋭角三角形をなすような $z$ の範囲を求め, 図示せよ。
問題1の解答
$z=1$ のときは三角形が成立しないので,以下では $z≠1$ とする。
平行移動は三角形の形を変えないので、-1 ずつ平行移動した3点 A’($0$), B’($z-1$), C’($z^2-1$) からなる△A’B’C’が鋭角三角形となればよい。
また,複素数の割り算は複素数平面上で相似拡大/縮小を伴う回転移動を表すから,
この3つの複素数を $z-1 (≠0)$ で割って3点 A’’ ($0$), B’’($1$), C’’($z+1$) をとったとき, △A’B’C’∽△A’’B’’C’’
(∵ A’B’:A’C’=A’’B’’:A’’C’’,∠B’A’C’=∠B’’A’’C’’より,二辺の比とその間の角が等しい)
さらに-1ずつ平行移動し,3点 D($-1$), E($0$), F ($z$) からなる△DEFが鋭角三角形となればよい。
∠D が鋭角となるための条件……( $z$ の実部)>-1
∠E が鋭角となるための条件……( $z$ の実部)<0
∠F が鋭角となるための条件……円周角を考えて,“点FがDEを直径とする円の外部にあること”
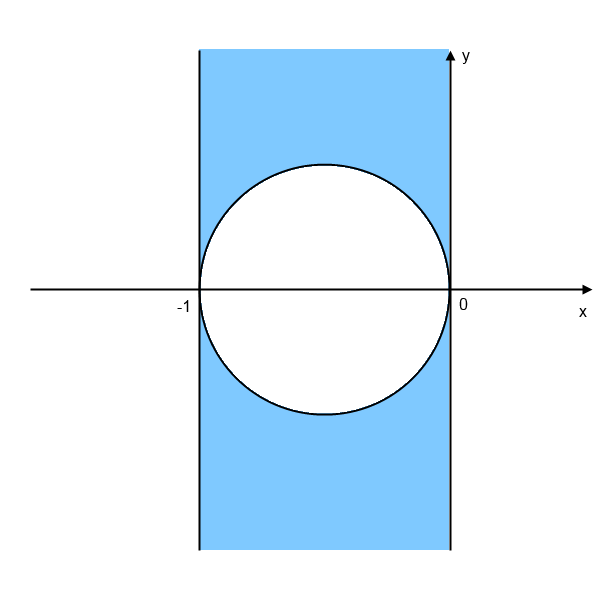
以上より,求める領域は下図の境界を含まない彩色部。
問題1のポイント,補足
・複素数の性質を活かした美しい解法を紹介しました。
・計算量は増えますが,普通に $z=x+yi$ とおき,内積を取るなどして鋭角であるための条件式を立てて整理していくことによっても解けます。むしろ,本番で点を取りに行く姿勢としてはそういう愚直なスタンスでいることを推奨します。
問題2
続いて2013年理系第1問です。
実数 $a,b$ に対し平面上の点 $P_n$ ($x_n, y_n$) を
($x_0, y_0$)=($1, 0$)
($x_{n+1}, y_{n+1}$)=($ax_n-by_n, bx_n+ay_n$) ($n=0,1,2,⋯$)
によって定める。このとき, 次の条件(ⅰ), (ⅱ)がともに成り立つような ($a, b$) をすべて求めよ。
(ⅰ) $P_0=P_6$
(ⅱ) $P_0, P_1, P_2, P_3, P_4, P_5$ は相異なる。
問題2の解答
複素数平面上で考え,$z_n=x_n+y_ni$ とおくと,
$z_{n+1}=(ax_n-by_n)+(bx_n+ay_n)i$
$=(a+bi)(x_n+y_ni)$
$=(a+bi) z_n$
∴ $z_6=(a+bi)^6z_0=z_0$ より,$(a+bi)^6=1$ となるので,$a+bi$ は 1 の 6 乗根
すなわち,$a+bi=\cos{\dfrac{kπ}{3}}+i\sin{\dfrac{kπ}{3}} (k=0,1,2,3,4,5)$
このうち,条件(ⅱ)を満たすものを考えて,$k=1,5$
∴ $(a,b)=(\dfrac{1}{2}, \dfrac{\sqrt{3}}{2}), (\dfrac{1}{2}, -\dfrac{\sqrt{3}}{2})$
問題2のポイント,補足
・2013年の出題当時は,複素数平面がまだ高校範囲でなく,旧課程の“一次変換”としての出題でした。
・“複素数平面”の問題としても解けるのですが,上の事情で“複素数平面”としての解答があまり見つからないということで,今回紹介しました。
・解答ではスマートに $z_{n+1}=(a+bi)z_n$ と式変形していますが,そこに至るまでには,
まず $P_n$ の遷移の規則を考える
⇒原点からの距離を調べてみる…… $\sqrt{a^2+b^2}$ 倍になっている
⇒多分回転と拡大・縮小の話だな……複素数の積の形で表せるのかな?
といった思考のステップを踏んでいます。つまり,状況把握の段階である程度“どうせ $\dfrac{π}{3}$ 回転だろう”という見当がついているからこそ,このように論を進められるのです。
複素数平面の問題は,東大では新課程で復活してからまだ1問しか出ていないので,東大入試の傾向というほどのものもまだないのですが,かつては難問もよく出題されていました。
一般論として,“図形的に攻めるか計算主体で行くか”の判断は意識的に行いましょう。
2016/05/12 石橋雄毅