今回は東大1983年の理系第6問のいろいろな解法を解説します。問題はかなり古いですが,良問です。最後に積分で体積を求める問題についての注意点を述べます。
問題
放物線$y=\dfrac{3}{4}-x^2$を$y$軸のまわりに回転して得られる曲面$K$を,原点を通り回転軸と$45^{\circ}$の角をなす平面$H$で切る。曲面$K$と平面$H$で囲まれた立体の体積を求めよ。
初手(全解答の共通部分)
曲面$K$の式は,$y=\dfrac{3}{4}-x^2-z^2$である。また,平面$H$の方程式は$y=x$としてもよい(このあたりは空間座標の基本的な知識が必要,東大を受験する理系なら短時間で突破したい)。
解答1:$z=t$で切る
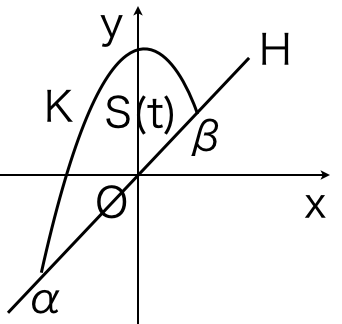
$z=t$で切った断面の面積$S(t)$を考える。曲面$K$と$z=t$の共通部分は$y=\dfrac{3}{4}-x^2-t^2$であり,平面$H$と$z=t$の共通部分は$y=x$である。よって,この放物線と直線で囲まれた図形の面積が$S(t)$である。放物線と直線の交点の$x$座標を$\alpha,\beta$とおくと,1/6公式より
$S(t)=\dfrac{|\beta-\alpha|^3}{6}$
一方,$\alpha,\beta$は二次方程式$x=\dfrac{3}{4}-x^2-t^2$の解なので,解と係数の関係より
$(\beta-\alpha)^2=(\alpha+\beta)^2-4\alpha\beta=1-4(t^2-\dfrac{3}{4})=-4t^2+4$
となる。以上から$S(t)=\dfrac{4}{3}(1-t^2)^{\frac{3}{2}}$
よって,求める体積は
$V=\int_{-1}^1S(t)dt=\dfrac{8}{3}\int_0^1(1-t^2)^{\frac{3}{2}}dt$
($\alpha=\beta$となるのが$t=\pm 1$であるときなので積分範囲が分かる)
あとは$t=\cos\theta$と置換して積分するのみ:
$V=-\dfrac{8}{3}\displaystyle\int_{\frac{\pi}{2}}^0\:\sin^3\theta\sin\theta d\theta\\=\displaystyle \dfrac{2}{3}\int_0^{\frac{\pi}{2}}(1-\cos 2\theta)^2d\theta\\=\dfrac{\pi}{2}$
最後の積分計算は少し省略しましたが,わりと簡単な計算です。
解答2:$x=t$で切る
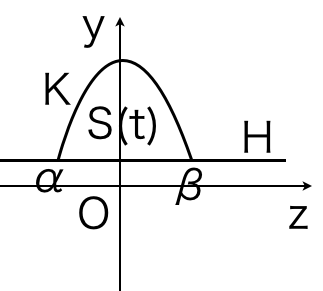
$x=t$で切った断面の面積$S(t)$を考える。曲面$K$と$x=t$の共通部分は$y=\dfrac{3}{4}-t^2-z^2$であり,平面$H$と$x=t$の共通部分は$y=t$である。放物線と直線の交点の$z$座標を$\alpha,\beta$とおくと,1/6公式より
$S(t)=\dfrac{|\beta-\alpha|^3}{6}$
一方,$\alpha,\beta$は二次方程式$t=\dfrac{3}{4}-t^2-z^2$の解なので,
$|\beta-\alpha|=2\sqrt{-t^2-t+\dfrac{3}{4}}$
よって,求める体積は
$V=\displaystyle\int_{a}^bS(t)dt=\dfrac{4}{3}\int_a^b(-t^2-t+\dfrac{3}{4})^{\frac{3}{2}}dt$
ただし,$a,b$は$-t^2-t+\dfrac{3}{4}=0$の解である,つまり$a=-\dfrac{3}{2},\:\:b=\dfrac{1}{2}$
これを積分する必要があるが,解答1よりはかなり難しい。ルートの中が二次式であることに注意して置換積分を行う。$t=-\dfrac{1}{2}+\cos\theta$と置換すると,ルートの中身は
$-(t+\dfrac{1}{2})^2+1=\sin^2\theta$
となるので,
$V=\dfrac{4}{3}\displaystyle\int_{\frac{\pi}{2}}^0\sin^3\theta\cdot(-\sin\theta)d\theta\\=\dfrac{8}{3}\displaystyle\int_0^{\frac{\pi}{2}}\sin^4\theta d\theta$
これは解答1と全く同じ式である。以下解答1と同様に積分すればOK。
解答3-1:$y=x+t$で切る
高校では習わない知識(正射影と面積の関係)を認めれば$y=x+t$で切っても計算できます。$y=x+t$で切った断面の面積$S(t)$を考える。曲面$K$と$y=x+t$の共通部分は$x+t=\dfrac{3}{4}-x^2-z^2$,つまり$(x+\dfrac{1}{2})^2+z^2=1-t$である。
この式は$xz$平面における円の方程式を表す。つまり,断面を$xz$平面に正射影すると半径$\sqrt{1-t}$の円になる。よって,
$S(t)=\sqrt{2}\pi (1-t)$
したがって,求める体積は,
$\int_0^1S(t)\cdot\dfrac{1}{\sqrt{2}}dt=\dfrac{\pi}{2}$
解答3-2:$y=x+t$で切る
回転放物面と平面の共通部分が楕円になることを認めれば,正射影を考えなくても$S(t)$が計算できます。計算の詳細は省略しますが,$y=x+t$で切った断面は長軸の長さが$2\sqrt{2}\sqrt{1-t}$,短軸の長さが$2\sqrt{1-t}$の楕円になるので,$S(t)=\sqrt{2}\pi (1-t)$となります。
積分で体積を求める問題について
・東大では積分を用いて立体の体積を求める問題が頻出です。この手の問題では切る方向が非常に重要になります。切る方向が不適切な場合,積分計算が非常に複雑になります(or計算出来ない)。どの方向から切るべきなのか考える時間は長めに取りましょう。
・立式しても終わりではありません。定積分の計算は非常にミスしやすいので,計算はかなり丁寧にしましょう。答案に途中式を細かく書くと検算もしやすいのでおすすめです。そして出てきた値が実際の立体の体積の値として妥当かどうかも確認しましょう。