第2問
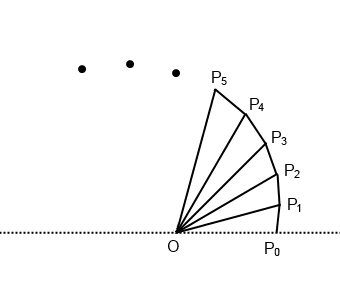
(1)
△OP
0P
1 ∽ △OP
1P
2 ∽ … となるから、相似比を考えて、
 ^{k-1}
)
余弦定理より、
^2 -2\left( 1 %2B \frac{1}{n} \right) \cos \frac{\pi}{n} }
)
であるから、
 ^{k-1}
)
 ・
・
 \sqrt{\pi ^2 %2B 1} ) ……(答)
……(答)
(2)
同様に、面積比を考えて、
 ^{2(k-1)}
)
 \times \sin \frac{\pi}{n}
)
であるから、
 ^{2(k-1)}
)
 ・
・
 ) ……(答)
……(答)
(3)
点 P
k の極からの距離は
 ^k
)
、
偏角は

(ただし、

より

)で表せる.
よって k を消去し、r と θ の関係を表せば、
 ^n \} ^{\frac{\theta}{\pi}} \to e^{\frac{\theta}{\pi}} \ \ \ (n \to \infty)
)
これは C 上の点の、極からの距離と偏角との関係を表した式に他ならない.
∴ C を表す極方程式は、 
) ……(答)
……(答)
(4)、(5)
与えられた積分に(3)で得られた

を代入して計算すれば、(1)、(2)と合わせて与式が成り立つことが示される.
せっかくの視覚化の機会なので、ちょっと作図してみました。
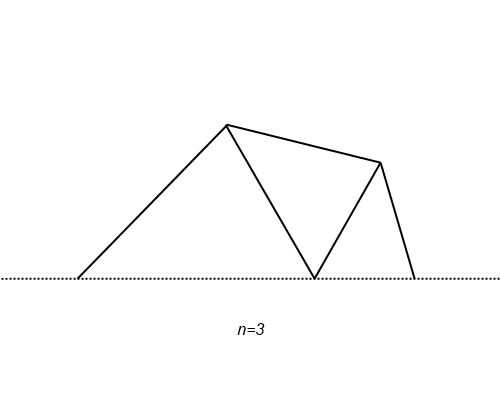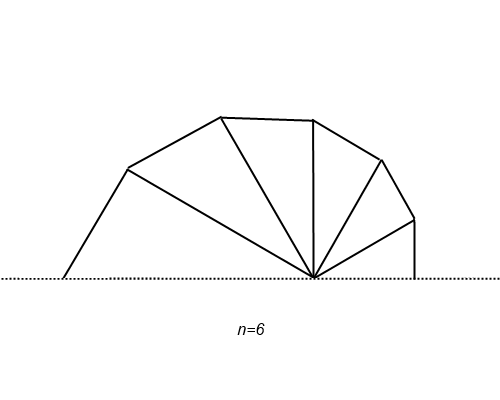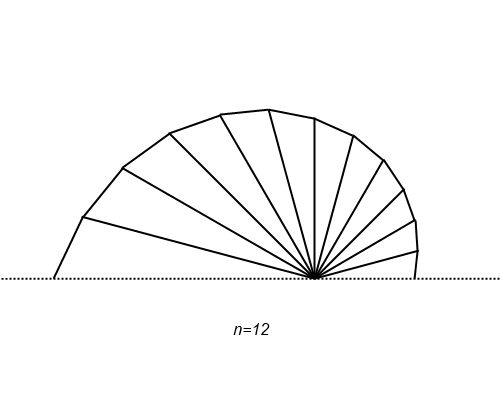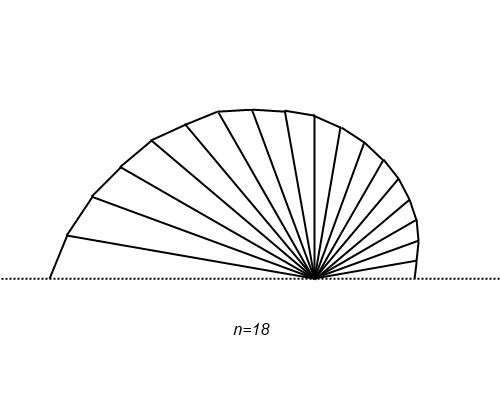


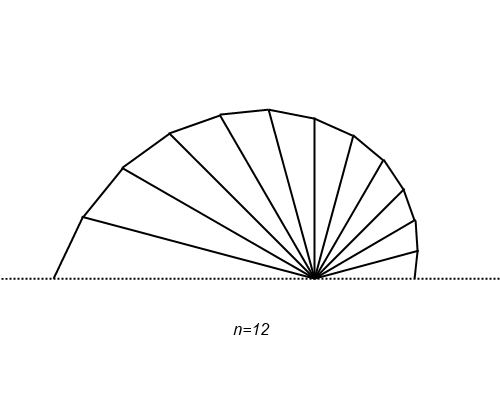
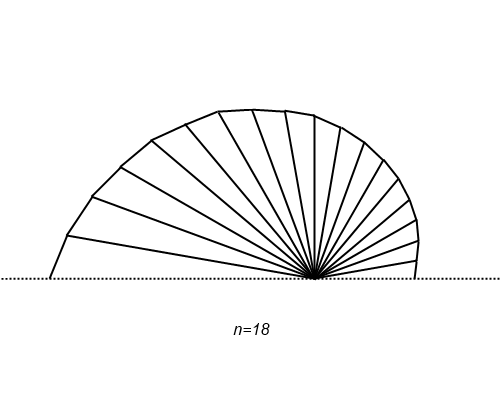
段々滑らかになって、ある曲線に収束する様子が確かめられますね。点 P
n の位置を見れば、自然対数の底 e の定義式が収束していく過程が増加しながらなのだということにも気が付きます(画像は n を不連続にしてしまっていますが、実際に確かめてみると単調増加します)。
⇒本文へ戻る