【対談その3】数学専門個別塾の塾長に聞く、数学の苦手克服法

こんにちは！東大入試ドットコム 編集長の林です。

数学というのは、苦手意識を持つ生徒が最も多い科目なんです。

入試で最も大きな点差がつく科目でもありますね。

東大を受験する生徒（特に理系）にとって、数学でいかに点をとるかが合格の鍵となります。

というわけで今回は、数学専門個別塾 MeTa の 春日さん に、数学の苦手克服法を伺いました。

難関大を目指したいけれど、数学がその邪魔をしている。

そんな人は必見です！

---

林　　東大入試ドットコムをご覧のみなさん、こんにちは！編集長の林です。対談企画第３弾、テーマは数学でございます。今日のゲストは、数学専門個別塾 MeTa の春日さんでございます。よろしくお願いします。

春日　はい、よろしくお願いします。

数学専門個別塾 MeTa とは

林　　さて、数学専門塾MeTaは、仙台にある塾なんですけども、まず簡単に自己紹介とか塾の紹介をして頂いてもよろしいですか？

春日　現在仙台市で高校生対象の数学専門塾 Meta を経営しております、春日幹雄と申します。数学専門の学習塾なんですけども、得意な子がもっと得意にするっていう風な数学専門塾ではなくて、ほんとに数学が苦手で、だけども大学入試に向けて克服したい、みたいな高校生対象の学習塾となっております。

林　　なるほど。結構、数学専門塾ってなかなか珍しいなと思います。よく幼稚園生とか小学生向けに、それこそパズルの塾とか算数教室とかありますけど、高校生とかに向けた数学塾ってあんまりないなと思いました。どうして数学塾って風にしようと思ったんですか？

春日　そうですね。やっぱりどの科目の中でも一番苦手となりやすいのって数学でして。やっぱり苦手科目の代名詞だと思うんですね。やっぱり数学が苦手で、例えば将来理系の方向に進みたいとか、看護師になりたい薬剤師になりたいみたいな夢を持ってるけども、数学が苦手で夢を諦めてしまうみたいな高校生が非常にたくさんいて。他の学習塾さんでも苦手克服に近い専門性を持った学習塾って少ないなと思って。こういう風に数学専門、苦手克服に絞っているって形に。

数学ができるだけで、大きな強みになる

林　　なるほど。なんとなく入試の対策を、じゃなくて。実際数学が苦手な子って多いみたいですね。数学の専門塾をやってらっしゃるということなんですけど…僕自身がそう思ってるんですが、入試だと数学ができるってだけでも結構強みになることってやっぱり多いんですかね。その辺どうなんでしょうね？

春日　そうですね。やっぱりまず配点は文系理系共にしっかり重視される。これって多分、難関大学になればなるほど、そういう傾向ありますよね。あとやっぱり英語とか他の科目に比べても一番点差が広がりやすいのかなって思って。英語だと、とりあえず和訳問題なので0点を取ることもなければ高得点を取るのも難しい。でも数学って1問1問が解ける解けないの勝負になってくる、やっぱり差もつきやすいし。なのでしっかりと数学を重視していくべきと考えております。

林　　確かに言われてみると、「爆死」する科目。確かに数学はそうだって印象はありますね。

数学攻略のカギは「目的意識」

林　　今日はせっかく数学がテーマなので、それこそ東大とか難関大受験生、数学が苦手な人に向けて役に立つ情報をと思っています。数学が苦手な子に共通していることってずばり何なんでしょう？

春日　そうですね。僕自身色々な高校生さん見させて頂いて1番思うのは、とにかく「意図」がないことだと思います。

林　　意図。

春日　数学を解くだけでなくても、何か他の科目を勉強してる時とかでも、とにかく意図を持たずに何となくやりすぎちゃっているような感じ。ただそこを改善できれば数学って克服できると考えております。

林　　なるほど。目的意識みたいな。

春日　そうですね。

林　　結構最近よく言われます。それこそよく微分とか積分とか言われても、あんまり生活に役に立つわけじゃないじゃないですか。学者なら別ですけど。なのになぜ勉強するのかとか結構モチベーション失っちゃう人も多いと思うんですけど。高校数学だったら、高校数学を勉強する意味ってどういうとこにあるんでしょう？

春日　そうですね。やっぱり三角関数とか微分積分って、日常生活であまり使わないですね。理系の大学に進むってなれば、また大学の勉強で使うと思うんですけど。文系入試でも課されている意義。数学を一般教養として見なされて選ばれてる意義って、論理的思考力を数学を通じて身に着けることで今後生きる力になっていくのかと考えております。論理的思考力って結構定義が曖昧でして。あまりしっかりとこういうことだよって、されていないんですけど。僕たちは現状と目標を照らし合わせて、意図を持って考える力っていう風に定義してます。

林　　なるほど。現状、論理的思考力って、少なくとも学校とかでそういう授業ってないじゃないですか。どういう時勉強するかっていうと、例えば就活とかでSPIって試験とかある。そういう時やるわけなんですけど。どうなんでしょう。そういう就活とかに限らず日常生活とかで役に立つものなんですか？

春日　そうですね。例えば部活とかでいきますと、例えばテニス部に入っていて、サーブ。なんとなくテニス部に入っていて、テニスを上手くなりたい。何も考えず練習しているよりかは、今現在現状、自分の現状でサーブが上手くないっていう風な現状をしっかりと把握したうえで、そこから目標を定義するべきだと思うんですよね。例えばあの先輩サーブ上手いなって考えて。じゃあその先輩を目標として、その先輩がサーブ上手い理由ってなんなんだろうってしっかり観察して。例えば腕の振り方が違うとか、ボールのトスの上げ方が違うとか。そういう風に目標と現状をしっかりと照らし合わせたうえで、じゃあボールトスの練習をしようとか、腕の振り方の練習をしようっていう風に意図が生まれて、やっと効率よく練習ってできるものなんです。そんな風に現状と目標を照らし合わせて、意図を発生させて、物事を解決させていくって、数学でも全く一緒の構図だと考えております。

林　　なるほど。日常生活の、それこそ部活みたいな例もありますし。その他人生で役に立つっていう。

例題（三角関数）で説明！

林　　どうなんでしょう。なんとなくああそうかみたいな感じで、ご覧の皆さんも思っていると思うんですよ。なのでできれば具体的に、こういう問題でなんでこういう計算をすんだとか、こういう思考をするんだとか、そういう風な例にして説明してもらえると実感がわくと思うので。何かその論理的思考力とか、例をちょっと示して頂いてもよろしいですか。

春日　待ってました。しっかりと書いてまして。今回高1高2生にもわかりやすいように少し問題の難易度下げているんですけど。この三角関数の y = cos^2θ - 2sinθ + 2 っていう式の最大値を求めろっていう風な問題にしますね。この問題、現状はこの式です。

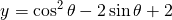
y の式があって目標が最大値なんです。じゃあこの現状と目標をしっかりと照らし合わせた結果どういう風にしたら最大値が求まるんだろうっていったん考えてほしくて。それで最大値って僕らってどうやって求められるかっていうと、微分とか、色々方法はあると思うんですけど。相加相乗とか。でも一番一般的なのは二次関数とかですね。二次関数としてグラフを描ければこの問題、最大値が求まるんです。っていう風な意図を持って。じゃあ二次関数にするためにこんな風な式変形が出てくるのかなと考えています。

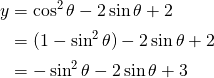
最終的に t = sinθ として、t の二次関数を出すことが目標なので、こんな風な式変形をしていくっていう風な発想が出てくるのかなって思っていて。問題1つ1つに対してこんな風に。これは応用問題になればなるほどなんですけど。現状の問題文と目標である出さなきゃいけない答えをしっかり照らし合わせた結果、どういう意図を発生させていくか、っていう風な考え方が大切だと思っています。

林　　なるほど。よっぽど変な問題はさておき、結構多くの問題、実はここはこういう風な思考のプロセスを経て出てきてるんだよみたいな、あるわけですね。発想を得られるようにする、言い方は変ですけど。そのようにするにはどういう勉強をすればいいんですかね？

春日　そうですね。例えば数学の問題集を解いてる時、答えを見て、ああこういう風にやれば解けるんだっていう風にしてその解法を覚えてしまうのではなくて。その解法ってどういうところからヒントを得て、どういうところから着想を得て、そういう発想になっているか。この公式をこのタイミングで使う理由って何だろう。この式変形をするのってなんでなんだっていう風に、発想っていう観点で色々と考え込んだり。どうしてもその発想法がわからなかったら先生方に質問して、っていう風なことで。その解法、問題の解説に書いてないことまでしっかりと掘り下げて、解答を読んでいくと定着するのかなと考えております。

林　　なるほど。この問題はこういう解法、この問題はこういう解法で場当たり的に見るんじゃなくて。1回1歩引いて。

春日　そうですね。

林　　どういう人なら、あるいはどういう思考をすればこういう解法が思いつくんだろうということを分析してみるといいですね。

数学が苦手な生徒へのメッセージ

林　　ありがとうございました。というわけで、今回は数学ということで、数学の苦手な人向けに数学専門塾 MeTa の春日さんから色々お話を伺いました。結構、それこそ東大入試とか、他の難関大入試を目指している人にとって数学ができればなって思ってる人たくさんいると思いますね。

春日　はい。

林　　最後にそういった方向けにメッセージをお願いしてもよろしいですか。

春日　そうですね。数学の苦手克服ってすんごい難しいんですよね。なんでなのかっていうと、まず1つ目に、小学校からの積み重ねなので。小中高っていう積み重ねなので、1回少しレールから外れてしまったり、苦手意識を持ってしまうと、できなくなったりしがちなんですよ。あと他には、他の科目とは違って暗記ではなく論理性を問われる科目なので、勉強法も少し変えていかなきゃいけないんですよね。なので、そういう風な工夫をしていかなきゃなかなか数学って克服できなくて。恐らくもうもすごい苦手な子って見ていられる方にもいると思うんですけど。でもしっかりと真摯に向き合って、今話した発想法だったり、っていう風なことを観点に勉強していけば確実に克服できます。実際僕の塾でもしっかりと克服してる子もいますので。しっかりと自分が得意になるビジョンを掲げながら前向きに取り組んでほしいですね。

林　　ありがとうございます。ということで、今回は以上でございますが、どうなんでしょう。仙台とかにお住まいの方であれば、数学専門塾 MeTa は通うことができるんですか？

春日　はい。ぜひとも。仙台市の仙台駅近くで行っております。

林　　ということで、もし東北にお住いの方であればぜひ行ってみてください。

春日　ありがとうございます。

林　　ということで、本日は以上でございます。数学専門塾 MeTa の春日さんとお届けしました。勉強頑張ってください〜！

春日　ありがとうございました！

数学専門個別塾 MeTa について

数学専門個別塾 MeTa は、仙台に校舎を構えています。

付近にお住まいの方はぜひお問い合わせをしてみてください！