【東大数学分野別解説】#16 難しくて奥が深い "軌跡・領域"

---

問 題 1

座標平面上の 1 点 $\mathrm{P}({\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{4}})$ をとる。放物線 $y=x^2$ 上の 2 点 $\mathrm{Q}(\alpha ,{\alpha }^2),\mathrm{R}(\beta ,{\beta }^2)$ を，3 点 $\mathrm{P},\mathrm{Q},\mathrm{R}$ が $\mathrm{Q}\mathrm{R}$ を底辺とする二等辺三角形をなすように動かすとき，$\mathrm{△}\mathrm{P}\mathrm{Q}\mathrm{R}$ の重心 $\mathrm{G}(X,Y)$ の軌跡を求めよ。

2011年 東大 文理共通問題

---

問 題 1 の 解 答

3 点 $\mathrm{P},\mathrm{Q},\mathrm{R}$ が三角形をなす，つまり "$\alpha \ne \beta ,\alpha \ne {\displaystyle \frac{1}{2}},\beta \ne {\displaystyle \frac{1}{2}}$ である" $\cdots (\ast )$ ことに注意する。

$(\ast )$ のもとで，3 点 $\mathrm{P},\mathrm{Q},\mathrm{R}$ が $\mathrm{Q}\mathrm{R}$ を底辺とする二等辺三角形をなすことは ${\mathrm{P}\mathrm{Q}}^2={\mathrm{P}\mathrm{R}}^2$ と同値であり，これを $\alpha ,\beta$ の式で表すと

$$\begin{array}{rl}& {\mathrm{P}\mathrm{Q}}^2={\mathrm{P}\mathrm{R}}^2\\ & \iff {(\alpha -{\displaystyle \frac{1}{2}})}^2+{({\alpha }^2-{\displaystyle \frac{1}{4}})}^2={(\beta -{\displaystyle \frac{1}{2}})}^2+{({\beta }^2-{\displaystyle \frac{1}{4}})}^2\\ & \iff ({\alpha }^4-{\beta }^4)+{\displaystyle \frac{1}{2}}({\alpha }^2-{\beta }^2)-(\alpha -\beta )=0\\ & \iff ({\alpha }^2+{\beta }^2)(\alpha +\beta )+{\displaystyle \frac{1}{2}}(\alpha +\beta )-1=0(\because \alpha \ne \beta )\end{array}$$

となる。

$\alpha ,\beta$ を用いると，$\mathrm{△}\mathrm{P}\mathrm{Q}\mathrm{R}$ の重心 $\mathrm{G}$ の座標 $(X,Y)$ は

$$\begin{array}{r}X=\frac{1}{3}(\alpha +\beta +\frac{1}{2}),Y=\frac{1}{3}({\alpha }^2+{\beta }^2+\frac{1}{4})\cdots (\circ )\end{array}$$

をみたすから，さきの二等辺の条件を $X,Y$ で表すと

$$\begin{array}{rl}& (3Y-{\displaystyle \frac{1}{4}})(3X-{\displaystyle \frac{1}{2}})+{\displaystyle \frac{1}{2}}(3X-{\displaystyle \frac{1}{2}})-1=0\\ & \iff (3X-{\displaystyle \frac{1}{2}})(3Y+{\displaystyle \frac{1}{4}})=1\end{array}$$

となる。また，2 式の組 $(\circ )$ は

$$\begin{array}{rl}& \{\begin{array}{l}\alpha +\beta =3X-{\displaystyle \frac{1}{2}}\\ {\alpha }^2+{\beta }^2=3Y-{\displaystyle \frac{1}{4}}\end{array}\\ & \iff \{\begin{array}{l}\alpha +\beta =3X-{\displaystyle \frac{1}{2}}\\ \alpha \beta ={\displaystyle \frac{1}{2}}{(3X-{\displaystyle \frac{1}{2}})}^2-{\displaystyle \frac{1}{2}}(3Y-{\displaystyle \frac{1}{4}})\end{array}\\ & \iff \{\begin{array}{l}\alpha +\beta =3X-{\displaystyle \frac{1}{2}}\\ \alpha \beta ={\displaystyle \frac{36X^2-12X+2-12Y}{8}}\end{array}\end{array}$$

と同値である。したがって，$\alpha ,\beta$ は $t$ の 2 次方程式

$$\begin{array}{r}{t}^2-(3X-{\displaystyle \frac{1}{2}})t+{\displaystyle \frac{36X^2-12X+2-12Y}{8}}=0\cdots (\mathrm{♢})\end{array}$$

の解である。$(\ast )$ も踏まえると，求める $(X,Y)$ の条件は "$\mathrm{P}\mathrm{Q}=\mathrm{P}\mathrm{R}$ であり，$t$ の 2 次方程式 $(\mathrm{♢})$ が相異なる 2 つの実数解をもち，かつそれらがいずれも ${\displaystyle \frac{1}{2}}$ と異なること" である。それを具体的に $(X,Y)$ に関する式として求めると

$$\begin{array}{rl}& \{\begin{array}{l}(3X-{\displaystyle \frac{1}{2}})(3Y+{\displaystyle \frac{1}{4}})=1\\ ((\mathrm{♢})\mathrm{の}\mathrm{判}\mathrm{別}\mathrm{式}\mathrm{の}\mathrm{値})>0\\ (t={\displaystyle \frac{1}{2}}\mathrm{で}\mathrm{の}(\mathrm{♢})\mathrm{の}\mathrm{左}\mathrm{辺}\mathrm{の}\mathrm{値})\ne 0\end{array}\\ & \iff \{\begin{array}{l}(3X-{\displaystyle \frac{1}{2}})(3Y+{\displaystyle \frac{1}{4}})=1\\ {(3X-{\displaystyle \frac{1}{2}})}^2-4\cdot 1\cdot {\displaystyle \frac{36X^2-12X+2-12Y}{8}}>0\\ {\left({\displaystyle \frac{1}{2}}\right)}^2-(3X-{\displaystyle \frac{1}{2}})\cdot {\displaystyle \frac{1}{2}}+{\displaystyle \frac{36X^2-12X+2-12Y}{8}}\ne 0\end{array}\\ & \iff \{\begin{array}{l}(3X-{\displaystyle \frac{1}{2}})(3Y+{\displaystyle \frac{1}{4}})=1\\ Y>{\displaystyle \frac{3}{2}}{(X-{\displaystyle \frac{1}{6}})}^2+{\displaystyle \frac{1}{12}}\\ Y\ne 3{(X-{\displaystyle \frac{1}{3}})}^2+{\displaystyle \frac{1}{6}}\end{array}\end{array}$$

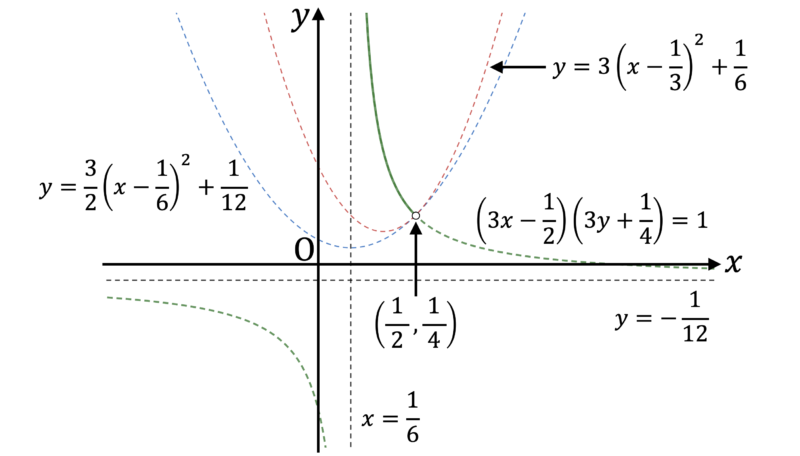
であり，これより重心 $\mathrm{G}$ の軌跡は次図の緑色の太線部のようになる。

---

問 題 1 の ポ イ ン ト ・ 補 足

文理共通での出題でしたが，初見で解くのはなかなか難しい問題だったはずです。
軌跡の問題では，文字消去をすることにより軌跡の必要条件を求めることが可能ですが，それだけでは軌跡を求めたことにはなりません。
文字消去により得られた曲線上の点の全てが軌跡に属するかを確認する必要があるためです。
本問でもまさに，直角双曲線の全部ではなく一部だけが軌跡となりました。

---

問 題 2

複素数 $a,b,c$ に対して整式 $f(z)=a{z}^2+bz+c$ を考える。$i$ を虚数単位とする。

(1) $\alpha ,\beta ,\gamma$ を複素数とする。$f(0)=\alpha ,f(1)=\beta ,f(1)=\gamma$ が成り立つとき，$a,b,c$ をそれぞれ $\alpha ,\beta ,\gamma$ で表せ。

(2) $f(0),f(1),f(i)$ がいずれも $1$ 以上 $2$ 以下の実数であるとき，$f(2)$ のとりうる範囲を複素数平面上に図示せよ。

2021年 東大 理系数学 第2問

---

問 題 2 の 解 答

(1) $f(0)=c,f(1)=a+b+c,f(i)=-a+bi+c$ より

$$\begin{array}{r}\{\begin{array}{l}\alpha =c\\ \beta =a+b+c\\ \gamma =-a+bi+c\end{array}\end{array}$$

であり，これより

$$\begin{array}{r}\{\begin{array}{l}a=-i\alpha +{\displaystyle \frac{1+i}{2}}\beta -{\displaystyle \frac{1-i}{2}}\gamma \\ b=(-1+i)\alpha +{\displaystyle \frac{1-i}{2}}\beta +{\displaystyle \frac{1-i}{2}}\gamma \\ c=\alpha \end{array}\end{array}$$

を得る。

(2)

(1) の結果を用いると

$$\begin{array}{rl}f(2)& =4a+2b+c\\ & =4\{i\alpha +{\displaystyle \frac{1+i}{2}}\beta -{\displaystyle \frac{1-i}{2}}\gamma \}\\ & +2\{(-1+i)\alpha +{\displaystyle \frac{1-i}{2}}\beta +{\displaystyle \frac{1-i}{2}}\gamma \}+\alpha \\ & =(-1-2i)\alpha +(3+i)\beta +(-1+i)\gamma \cdots (\mathrm{こ}\mathrm{れ}\mathrm{を}w\mathrm{と}\mathrm{す}\mathrm{る})\end{array}$$

となるから，$\alpha ,\beta ,\gamma$ が各々 $1$ 以上 $2$ 以下の実数を動くときに，複素数 $w$ の動く範囲を求めればよいが，${\alpha }^{\prime }:=\alpha -1,{\beta }^{\prime }=\beta -1,{\gamma }^{\prime }=\gamma -1$ とすることで

$$\begin{array}{rl}w& =(-1-2i)\alpha +(3+i)\beta +(-1+i)\gamma \\ & =(-1-2i)({\alpha }^{\prime }+1)+(3+i)({\beta }^{\prime }+1)+(-1+i)({\gamma }^{\prime }+1)\\ & =(-1-2i){\alpha }^{\prime }+(3+i){\beta }^{\prime }+(-1+i){\gamma }^{\prime }+1\end{array}$$

と変形できるので，${\alpha }^{\prime },{\beta }^{\prime },{\gamma }^{\prime }$ が $0$ 以上 $1$ 以下の実数を動くときの複素数 $w$ の動く範囲もさきの範囲と同じであり，これを求めることとする。

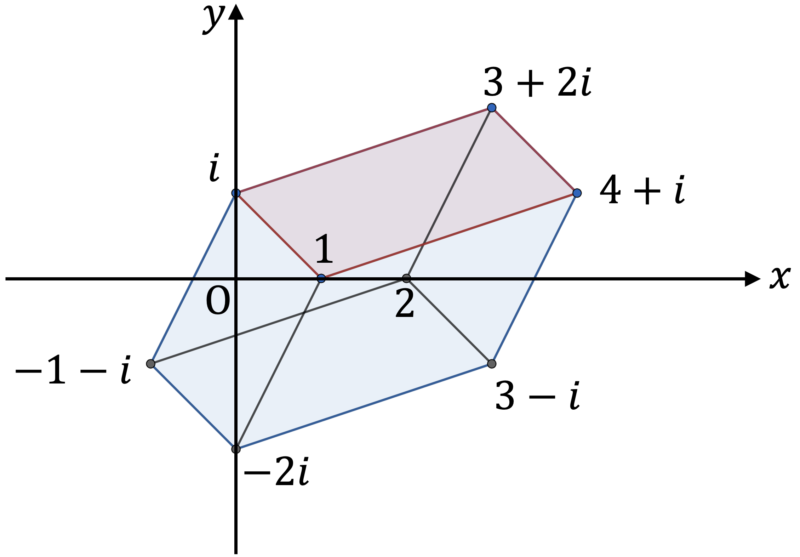
まず $\alpha =0$ と固定すると $w=(3+i){\beta }^{\prime }+(-1+i){\gamma }^{\prime }+1$ と書ける。${\beta }^{\prime },{\gamma }^{\prime }$ が各々 $0$ 以上 $1$ 以下の実数を自由に動くと，$w$ は複素数 $1$, $1+(3+i)=4+i$, $1+(-1+i)=i$, $1+(3+i)+(-1+i)=3+2i$ を頂点とした平行四辺形の周および内部を動く。

次に $\alpha$ を $0$ 以上 $1$ の範囲で動かすと，$w$ の動く範囲はさきの平行四辺形を $-1-2i$ 平行移動したときにこれが通過する領域であることがわかり，具体的に図示すると次の通り。

---

問 題 2 の ポ イ ン ト ・ 補 足

逆像法ばかり扱っていると，図形をそのまま動かして領域を求めるというアプローチを忘れてしまうかもしれません。
本問も逆像法で答えを出すことはできるでしょうが，このように図形をそのまま動かしてしまう方が明快だと思います。(曲線的な移動が全くありませんので。)
本問のほかにも，2019年の文系数学第4問で，図形を動かして領域を求める問題が出題されています。

---

問 題 3

座標平面の原点を O で表す。線分 $y=\sqrt{3}x(0\leqq x\leqq 2)$ 上の点 $\mathrm{P}$ と，線分 $y=-\sqrt{3}x(-3\leqq x\leqq 0)$ 上の点 $\mathrm{Q}$ が，線分 $\mathrm{O}\mathrm{P}$ と線分 $\mathrm{O}\mathrm{Q}$ の長さの和が $6$ となるように動く。このとき，線分 $\mathrm{P}\mathrm{Q}$ の通過する領域を $D$ とする。

(1) $s$ を $-3\leqq s\leqq 2$ をみたす実数とするとき，点 $(s,t)$ が $D$ に入るような $t$ の範囲を求めよ。

(2) $D$ を図示せよ。

2014年 東大 文系数学 第3問

---

問 題 3 の 解 答

線分 $\mathrm{P}\mathrm{Q}$ の存在範囲は $y\geqq \mathrm{m}\mathrm{a}\mathrm{x}\{\sqrt{3}x,-\sqrt{3}x\}$ に限られるが，まず線分ではなく直線 $\mathrm{P}\mathrm{Q}$ の通過領域を考え，最後に $-3\leqq x\leqq 1$ および $y\geqq \mathrm{m}\mathrm{a}\mathrm{x}\{\sqrt{3}x,-\sqrt{3}x\}$ の条件を課したものを求めることとする。(※ここが地味ながら重要なポイントです。)

点 $\mathrm{P}$ の座標を $(p,\sqrt{3}p)(0\leqq p\leqq 2)$ とする。$\mathrm{O}\mathrm{P}+\mathrm{O}\mathrm{Q}=6$ より点 $\mathrm{Q}$ の $x$ 座標は $p-3$ となる。ここで $-3\leqq p-3\leqq -1$ となるため，$p$ の動く範囲は単に $0\leqq p\leqq 2$ としてよい。点 $\mathrm{Q}$ の座標が $(p-3,-\sqrt{3}(p-3))$ であるため，直線 $\mathrm{P}\mathrm{Q}$ の方程式は

$$\begin{array}{rl}& y-\sqrt{3}p=\frac{\sqrt{3}p-(\sqrt{3}(p-3))}{p-(p-3)}(x-p)\\ & \iff y=\frac{1}{\sqrt{3}}(2p-3)x+\frac{1}{\sqrt{3}}(-2p^2+6p)\end{array}$$

である。この $x$ の値を $s$ に固定し，$p$ を動かしたときの $y$ の値域を求める。

$x=s$ として $y$ を $p$ の関数として整理すると

$$\begin{array}{rl}y& =\frac{1}{\sqrt{3}}(2p-3)x+\frac{1}{\sqrt{3}}(-2p^2+6p)\\ & =-\frac{2}{\sqrt{3}}{(p-\frac{3}{2}(1+\frac{1}{3}s))}^2+\frac{3\sqrt{3}}{2}{(1+\frac{1}{3}s)}^2-\sqrt{3}s\\ & =-\frac{2}{\sqrt{3}}{(p-\frac{3}{2}(1+\frac{1}{3}s))}^2+\frac{3\sqrt{3}}{2}(1+\frac{1}{9}{s}^2)\end{array}$$

となる (最右辺を $f(p)$ とおく)。

$p$ を制限しないときに $y$ が最大となるのは $p={\displaystyle \frac{3}{2}}(1+{\displaystyle \frac{1}{3}}s)$ のとき (この値を $p^{\ast }$ とする) であるが，この値が $0\leqq p\leqq 2$ に入るのは

$$\begin{array}{r}0\leqq {\displaystyle \frac{3}{2}}(1+{\displaystyle \frac{1}{3}}s)\leqq 2\therefore -3\leqq s\leqq 1\end{array}$$

のときである。また，$f(0)$ と $f(2)$ の大小関係が入れ替わるのは

$$\begin{array}{r}(1+{\displaystyle \frac{1}{3}}s)=1\therefore s=0\end{array}$$

のときである。以上を踏まえ，$s=0,1$ を境に場合分けすることにより $f(p)(0\leqq p\leqq 2)$ の最大値 $f_{\mathrm{m}\mathrm{a}\mathrm{x}}$・最小値 $f_{\mathrm{m}\mathrm{i}\mathrm{n}}$ を求める。ただし，冒頭で述べた通り線分 $\mathrm{P}\mathrm{Q}$ の存在範囲が $y\geqq \mathrm{m}\mathrm{a}\mathrm{x}\sqrt{3}x,-\sqrt{3}x$ に限られることに注意する。

(i) $-3\leqq s\leqq 0$ のときは，$f_{\mathrm{m}\mathrm{a}\mathrm{x}}=f(p^{\ast })={\displaystyle \frac{3\sqrt{3}}{2}}(1+{\displaystyle \frac{1}{9}}{s}^2)$，$f_{\mathrm{m}\mathrm{i}\mathrm{n}}=f(2)={\displaystyle \frac{4+s}{\sqrt{3}}}$ となる。またこのとき $f_{\mathrm{m}\mathrm{i}\mathrm{n}}\leqq -\sqrt{3}s$ である。

(ii) $0\leqq s\leqq 1$ のときは，$f_{\mathrm{m}\mathrm{a}\mathrm{x}}=f(p^{\ast })={\displaystyle \frac{3\sqrt{3}}{2}}(1+{\displaystyle \frac{1}{9}}{s}^2)$，$f_{\mathrm{m}\mathrm{i}\mathrm{n}}=f(0)=-\sqrt{3}s$ となる。またこのとき $f_{\mathrm{m}\mathrm{i}\mathrm{n}}\leqq \sqrt{3}s$ である。

(iii) $f_{\mathrm{m}\mathrm{a}\mathrm{x}}=f(2)={\displaystyle \frac{4+s}{\sqrt{3}}}$，$f_{\mathrm{m}\mathrm{i}\mathrm{n}}=f(0)=-\sqrt{3}s$ となる。またこのとき $f_{\mathrm{m}\mathrm{i}\mathrm{n}}\leqq \sqrt{3}s$ である。

点 $(s,t)$ が $D$ に入るための条件は以下の通り。

$$\begin{array}{r}\{\begin{array}{l}-3\leqq s\leqq 0\mathrm{の}\mathrm{と}\mathrm{き}-\sqrt{3}s\leqq t\leqq {\displaystyle \frac{3\sqrt{3}}{2}}(1+{\displaystyle \frac{1}{9}}{s}^2)\\ 0\leqq s\leqq 1\mathrm{の}\mathrm{と}\mathrm{き}\sqrt{3}s\leqq t\leqq {\displaystyle \frac{3\sqrt{3}}{2}}(1+{\displaystyle \frac{1}{9}}{s}^2)\\ 1\leqq s\leqq 2\mathrm{の}\mathrm{と}\mathrm{き}\sqrt{3}s\leqq t\leqq {\displaystyle \frac{4+s}{\sqrt{3}}}\end{array}\end{array}$$

(2)

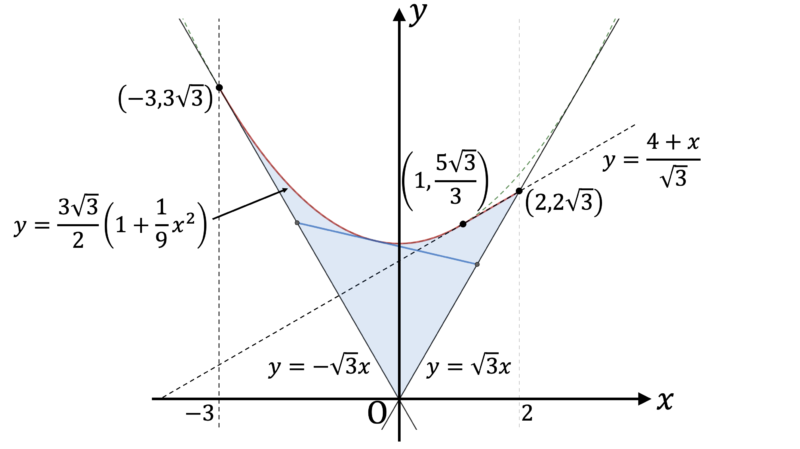
(1) の結果の範囲 ($D$) を図示すると次のようになる。境界は全て含む。

---

問 題 3 の ポ イ ン ト ・ 補 足

難関大対策の数学を勉強していると，逆像法が目立ち気味で，本問のようにシンプルな順像法が思いつかないかもしれません。ただ，考えてもみれば軌跡・領域を求める基本 (自然な手順？) は順像法なので，まずはこれをしっかり勉強すべきなのかもしれませんね。
ほかにも，2015 年度の理系数学第 1 問が順像法による攻略が可能です。

"直線 $\mathrm{P}\mathrm{Q}$" ではなく "線分 $\mathrm{P}\mathrm{Q}$" の通過領域となっているのが厄介ですが，$-3\leqq s\leqq 1$ の範囲でまず "直線 $\mathrm{P}\mathrm{Q}$" の通過領域を考え，あとで $y\geqq \mathrm{m}\mathrm{a}\mathrm{x}\{-\sqrt{3}x,\sqrt{3}x\}$ という範囲を課して V 字にカットするという方針をとることで，面倒な議論を省略できます。

---

参考問題

東大の数学では，軌跡・領域の問題がほかにも多数出題されています。
参考までに，いくつか問題例を載せておきます。

1 辺の長さが 1 の正六角形 $\mathrm{A}\mathrm{B}\mathrm{C}\mathrm{D}\mathrm{E}\mathrm{F}$ が与えられている。点 $\mathrm{P}$ が辺 $\mathrm{A}\mathrm{B}$ 上を，点 $\mathrm{Q}$ が辺 $\mathrm{C}\mathrm{D}$ 上をそれぞれ独立に動くとき，線分 $\mathrm{P}\mathrm{Q}$ を $2:1$ に内分する点 $\mathrm{R}$ が通りうる範囲の面積を求めよ。

2017年 東大 文系数学 第2問

$a,b$ を実数の定数とする。実数 $x,y$ が

$$\begin{array}{r}{x}^2+y^2\leqq 25,2x+y\leqq 5\end{array}$$

をともに満たすとき，$z=x^2+y^2-2ax-2by$ の最小値を求めよ。

2013年 東大 文系数学 第3問

座標平面上の 2 点 $\mathrm{P},\mathrm{Q}$ が，曲線 $y=x^2(-1\leqq x\leqq 1)$ 上を自由に動くとき，線分 $\mathrm{P}\mathrm{Q}$ を $1:2$ に内分する点 $R$ が動く範囲を $D$ とする。ただし，$\mathrm{P}=\mathrm{Q}$ のときは $\mathrm{R}=\mathrm{P}$ とする。

(1) $a$ を $-1\leqq a\leqq 1$ をみたす実数とするとき，点 $(a,b)$ が $D$ に属するための $b$ の条件を $a$ を用いて表せ。

(2) $D$ を図示せよ。

2007年 東大 理系数学 第3問

---

まとめ 〜軌跡・領域のポイント〜

今回は，

• 問題１：逆像法
• 問題２：順像法（図形を動かす）
• 問題３：順像法（関数の値域を求める）

という 3 パターンの問題をご紹介してみました。

軌跡・領域の問題は大変奥深く，難易度も高めになりがちです。
その分差がつきやすい分野でもあるので，高校数学の未習範囲がなくなり，基礎的な力が付いてきたらぜひ重点的に対策してみてください。
さまざまな種類の問題を解いたり，同じ問題を複数のアプローチで解いてみると，理解が深まることでしょう。