【東大数学分野別解説】#15 東大で頻出の "不等式"

2022.03.10

この連載では，東大数学の過去問の中から学びの多そうなものを分野別に解説していきます。単に正解を述べるだけでなく，問題を解く際のアプローチや補足事項も添えるので，初見の問題への対応力も磨けることでしょう。

不等式に関連する問題は，東大をはじめとする難関大学の入試で頻出です。
不等式で領域が指定され，それを図示したりその範囲におけるある関数の最大値を問われることもあれば，不等式を証明したり，式が成り立つパラメータの範囲を問われることもあり，内容は実に様々です。
今回は

不等式で領域が指定されており，そこにおける最大値・最小値を考える問題
不等式が成り立つパラメータの範囲を求める問題

をご紹介します。

問題 1

$a$ を正の実数とする。次の 2 つの不等式を同時にみたす点 $(x, \, y)$ 全体からなる領域を $D$ とする。
$$
\begin{align}
y \geqq x^2, \quad y \leqq - 2x^2 + 3ax + 6a^2
\end{align}
$$
領域 $D$ における $x+y$ の最大値，最小値を求めよ。
2004年度東大文系数学第2問

問題 1 の解答

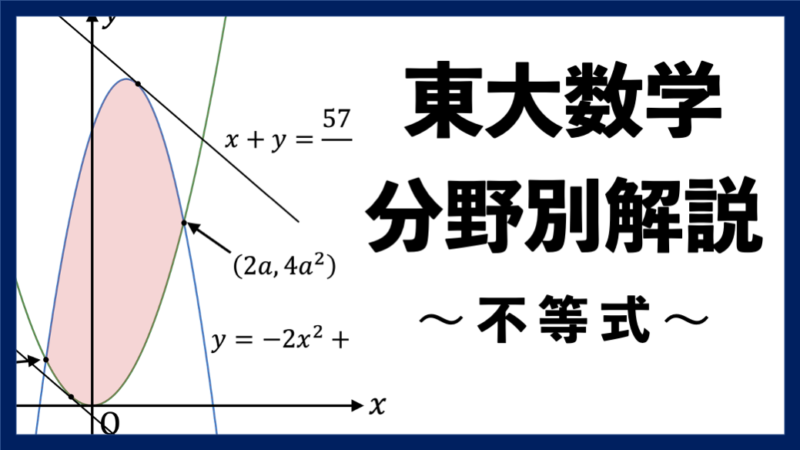
放物線 $y = x^2$ を $C_{1}$, 放物線 $y = -2x^2 + 3ax + 6a^2$ を $C_{2}$ とする。$C_{1}$ と $C_{2}$ の交点の $x$ 座標を求めると, $x^2 = -2x^2 + 3ax + 6a^2$ より $x = -a, \, 2a$ であるため, 2 つの放物線の交点は $(-a, \, a^2)$ および $(2a, \, 4a^2)$ である。ここで, 直線 $l: \, x + y = k$ ($k$ は定数) を考え, これが領域 $D$ と共有点をもつような $k$ の最大値・最小値を求めれば, それが本問で問われている $x+y$ の最大値・最小値となっている。

▶︎ $k$ の最大値

$k$ が最も大きくなるのは, $l$ が $C_{2}$ と接するときまたは $l$ が点 $(2a, \, 4a^2)$ を通るときである。$l$ と $C_{2}$ が接するとき, それら 2 つの方程式を連立して得られる二次方程式 $-2x^2 + 3ax + 6a^2 = -x + k$ が重解をもてばよいので, $( {\rm 判別式の値} ) = 0$ から $k=\displaystyle \frac{57a^2 + 6a + 1}{8}$ となる。また, このときの重解は $x = \displaystyle \frac{3a+1}{4}$ であり, これは接点の $x$ 座標にほかならない。

この接点が領域 $D$ 上に (より詳しくいえば, 領域 $D$ の周上に) 存在するならば, $k$ はそのときに最大となる。領域 $D$ 上にあることの必要十分条件は $\displaystyle \frac{3a+1}{4} \leqq 2a$ すなわち $a \geqq \displaystyle \frac{1}{5}$ であるから, $a$ がこの範囲にあるときの $k(=x+y)$ の最大値は $\displaystyle \frac{57a^2 + 6a + 1}{8}$ である。

一方, さきの接点が領域 $D$ 上にないとき, つまり $a < \displaystyle \frac{1}{5}$ のときは, $l$ が点 $(2a, \, 4a^2)$ を通るときに $k \, (= x+y)$ が最大となり, その最大値は $4a^2 + 2a$ である。

以上をまとめると，

$$
\begin{align}
(x+y \,{\rm の最大値}) =
\begin{cases}
\displaystyle \frac{57a^2 + 6a + 1}{8} \quad \left(a \geqq \frac{1}{5} {\rm のとき} \right) \\
4a^2 + 2a \hspace{11mm} \quad \left( 0 < a < \displaystyle \frac{1}{5} {\rm のとき} \right)
\end{cases}
\end{align}
$$

となる。

▶︎ $k$ の最小値

$k$ が最も小さくなるのは, $l$ が $C_{1}$ と接するときまたは $l$ が点 $(-a, \, a^2)$ を通るときである。$l$ と $C_{1}$ が接するとき, それら 2 つの方程式を連立して得られる二次方程式 $x^2 = -x + k$ が重解をもてばよいので, $({\rm 判別式}) = 0$ から $k=-\displaystyle \frac{1}{4}$ となる。また, このときの重解は $x = -\displaystyle \frac{1}{2}$ であり, これは接点の $x$ 座標にほかならない。

この接点が領域 $D$ 上に存在するならば, $k$ はそのときに最大となる。領域 $D$ 上にあることの必要十分条件は $-\displaystyle \frac{1}{2} \geqq -a$ すなわち $a \geqq \displaystyle \frac{1}{2}$ であるから, $a$ がこの範囲にあるときの $k \, (=x+y)$ の最大値は $-\displaystyle \frac{1}{4}$ である。

一方, さきの接点が領域 $D$ 上にないとき, つまり $a < \displaystyle \frac{1}{2}$ のときは, $l$ が点 $(-a, \, a^2)$ を通るときに $k \, (= x+y)$ は最大となり, その最大値は $a^2 - a$ である。

以上をまとめると，

$$
\begin{align}
(x+y \,{\rm の最小値}) =
\begin{cases}
\displaystyle \frac{1}{4} \hspace{5mm} \quad \left( a \geqq \frac{1}{2} {\rm のとき} \right) \\
a^2 - a \quad \left( 0 < a < \displaystyle \frac{1}{2} {\rm のとき} \right)
\end{cases}
\end{align}
$$

となる。

問題 1 のポイント・補足

難関大入試で頻出の最大値・最小値問題でした。

解説では直線 $x+y=k$ と領域 $D$ が共有点をもつような $k$ の値の範囲を求めるという方針をとりました。
おそらくどの参考書でもこの解法がメインで扱われている，またはこの解法しか載っていないのではないでしょうか。

ただ，これしか解法がないわけではありません。
たとえば領域 $D$ において $x$ 座標を固定すると，$x + y$ が最大となるのは $y$ が最大である点になり，$x+y$ が最小となるのは $y$ が最小である点になります。
つまり，$x$ 座標を固定してできる縦線上で "予選" を行い，次に $x$ 座標を $-a \leqq 2a$ の範囲で動かすことで "決勝" を行うという解法もあります。
これはこれでわかりやすい (もしかしたらこの方が簡単？) ので，興味のある人はぜひこの解法も研究してみてください。

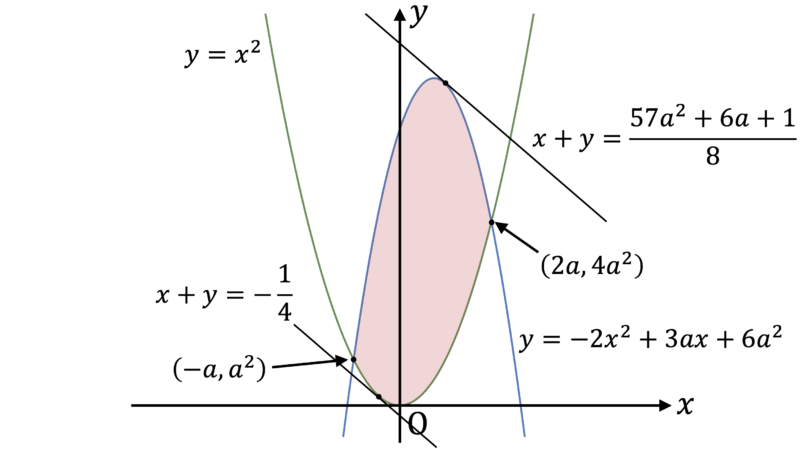
なお，$a$ の値に応じて，$x+y$ の値が最大・最小となる点は次のように変化します。

▶︎ $a \geqq \dfrac{1}{2}$ のとき

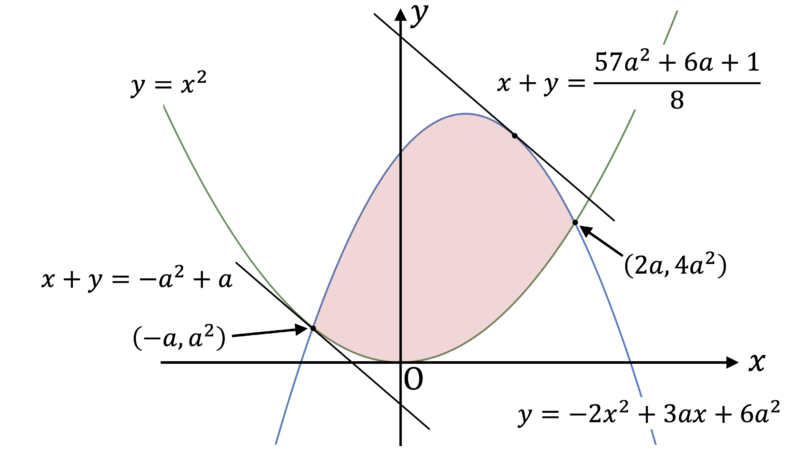
▶︎ $\dfrac{1}{5} \leqq a \leqq \dfrac{1}{2}$ のとき

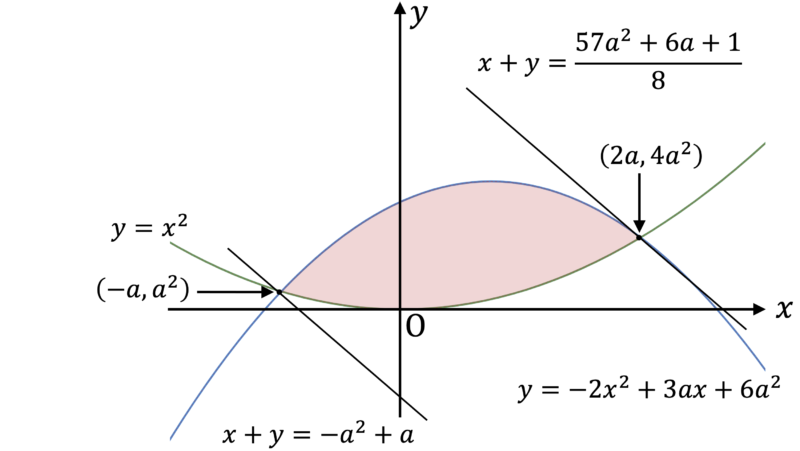
▶︎ $a \leqq \dfrac{1}{5}$ のとき

大まかにで構いませんので，自分で問題演習をするときも積極的に図を描くようにしましょう。
もちろん，今回の境界値である $a = \dfrac{1}{5}, \, \dfrac{1}{2}$ といった値まではわかりませんが，$a$ が小さいと "両端" が最大点・最小点になり，$a$ が大きいと放物線の途中に最大点・最小点が発生することが予想できます。
それがわかるだけでも，答案作成はだいぶやりやすくなるはずです。

問題 2

すべての正の実数 $x, \, y$ に対し
$$
\begin{align}
\sqrt{x} + \sqrt{y} \leqq k \sqrt{2x + y}
\end{align}
$$
が成り立つような実数 $k$ の最小値を求めよ。
1995年東大文理共通問題

問題 2 の解答

左辺が正なので $k \geqq 0$ に限定して考える。

$\sqrt{\displaystyle \frac{y}{\, x \,}} = t$ とおく。任意の正の実数に対し不等式 $1 + t \leqq k \sqrt{2 + t^2}$ が成り立てばよい。両辺はいずれも正なので，両辺の 2 乗の差

\begin{eqnarray}
k^2 (2 + t^2) - (1 + t)^2 = (k^2 - 1) t^2 - 2t + (2k^2 - 1) \quad \cdots ({\rm A})
\end{eqnarray}

が任意の正の実数 $t$ に対し 0 以上であればよい。そこで (${\rm A}$) の右辺を $f(t)$ とする。$k \leqq 1$ の場合は十分に大きい $t$ に対し (${\rm A}$) が成り立たなくなるため，$k > 1$ の場合を考える。このとき $f(t)$ は 2 次の係数が正の 2 次関数であり，$k > 1$ より $f(0) > 0$ である。$f(t)$ を平方完成すると

\begin{eqnarray}
f(t) = (k^2 - 1) \left( t - \frac{1}{\, k^2 - 1 \,} \right)^2 + \left( 2k^2 - 1 - \frac{1}{\, k^2 - 1 \,} \right) \geqq 0
\end{eqnarray}

となり，各 $k$ に対し $f(t)$ は $t = \displaystyle \frac{1}{\, k^2 - 1 \,} \, (>0)$ で最小値 $2k^2 - 1 - \displaystyle \frac{1}{\, k^2 - 1 \,}$ をとるため，これが 0 以上となれば必要十分である。よって条件をみたす $k$ の範囲は

\begin{eqnarray}
2k^2 - 1 - \displaystyle \frac{1}{\, k^2 - 1 \,} \geqq 0 \quad &\Leftrightarrow& \quad 2k^2 - 1 \geqq \frac{1}{\, k^2 - 1 \,} \\
&\Leftrightarrow& \quad (2k^2 - 1)(k^2 - 1) \geqq 1 \\
&\Leftrightarrow& \quad k^2 \geqq \frac{3}{\, 2 \,} \quad (\because k \neq 0) \\
&\Leftrightarrow& \quad k \geqq \sqrt{\frac{3}{\, 2 \,}} = \frac{\, \sqrt{6} \,}{2}
\end{eqnarray}

となり，これをみたす $k$ で最も小さいものは $\underline{k = \displaystyle \frac{\, \sqrt{6} \,}{2}}$ である。

問題 2 の別解

特に $x = 1, \, y = 4$ でも不等式が成り立たなければならないため，

\begin{eqnarray}
\sqrt{1} + \sqrt{4} \leqq k \sqrt{2 \cdot 1 + 4} \quad \therefore k \geqq \frac{\sqrt{6}}{2}
\end{eqnarray}

が必要である。逆に $k = \dfrac{\sqrt{6}}{2}$ のとき，

$$
\begin{align}
&{} \left( \frac{\sqrt{6}}{2} \sqrt{2x + y} \right)^2 - \left( \sqrt{x} + \sqrt{y} \right)^2 \\
&= \frac{3}{2} \left( 2x + y \right) - \left( x + 2 \sqrt{xy} + y \right) \\
&= 2x - 2 \sqrt{xy} + \frac{1}{2} y \\
&= \left( \sqrt{2x} - \sqrt{\frac{y}{2}} \right)^2 \geqq 0
\end{align}
$$

であり，問題文の不等式の両辺は正であるため，任意の正の実数 $x, \, y$ に対し $\sqrt{x} + \sqrt{y} \leqq \dfrac{\sqrt{6}}{2} \sqrt{2x + y}$ が成り立つ。

以上より，求める最小値は $k = \dfrac{\sqrt{6}}{2}$ である。

問題 2 の別解 (理系向け)

任意の正の実数 $x, \, y$ に対し

$$
\begin{align}
\frac{\sqrt{x} + \sqrt{y}}{\sqrt{2x + y}} \leqq k
\end{align}
$$

が成り立つような実数 $k$ の最小値を求めればよい。$t := \dfrac{y}{x}$ とすると，上の不等式の左辺は

$$
\begin{align}
\frac{\sqrt{x} + \sqrt{y}}{\sqrt{2x + y}} = \frac{1 + \sqrt{\dfrac{y}{x}}}{2 + \dfrac{y}{x}} = \frac{1 + \sqrt{t}}{\sqrt{2 + t}}
\end{align}
$$

と変形できる。最右辺を $t$ の関数とみて $f(t)$ とおくと，

$$
\begin{align}
f'(t) &= \frac{1}{\sqrt{2 + t}^2} \left\{ \frac{1}{2 \sqrt{t}} \cdot \sqrt{2 + t} - \left( 1 + \sqrt{t} \right) \cdot \frac{1}{2 \sqrt{2+t}} \right\} \\
&= \cdots = \frac{2 - \sqrt{t}}{2 \sqrt{2+t}^3 \sqrt{t}}
\end{align}
$$

となり，$t > 0$ において $f'(t) = 0$ となるのは $t = 4$ のときのみとわかる。$0 < \sqrt{t} < 4$ において $f'(t) > 0$，$4 < \sqrt{t}$ において $f'(t) < 0$ であることを踏まえると，$t > 0$ における $f(t)$ の最大値は

$$
\begin{align}
f_{{\rm max}} = f\left( 4 \right) = \frac{1 + \sqrt{4}}{2 + 4} = \frac{\sqrt{6}}{2}
\end{align}
$$

である。以上より，条件をみたす $k$ の最大値は $k = \dfrac{\sqrt{6}}{2}$ とわかる。

問題 2 のポイント・補足

問題文がシンプルなこともあり，東大の過去問の中でも有名なもののひとつです。

問題文の不等式は変数が $x, \, y$ の 2 つありますが，どの項も $x, \, y$ の次数が等しくなっています。よって，両辺を $\sqrt{x}$ や $\sqrt{y}$ で割り算することにより，実質的な変数を 1 つ減らすことができるというわけです。
これに気づけるかどうかが明暗を分つのではないでしょうか。

別解を複数述べましたが，このように本問は様々な方法で解くことができ，不等式の問題演習をするうえで大変よい題材となります。
一部の別解以外は数学III の知識を必要としないため，文系数学範囲の勉強が終わった人はぜひチャレンジしてみてください！

なお，1 つ目の別解では $(x, \, y) = (1, \, 4)$ という値の組を唐突に出しましたが，この値をどうやって見つけたかについても，興味のある人は考えてみてください。