【東大数学分野別解説】#12 不等式の証明と利用がセットの "指数・対数"

東大入試では，指数関数や対数関数が単体で大問になっているものはあまりみられませんが，(1) で不等式の証明をし，(2) でそれを利用してある関係式の成立を示したり極限を求めたりする問題は，主に理系で登場します。
今回は，その中でも解きごたえのあるものを 2 問選びました。

---

問 題 1

複素数 $z_{n} \, (n = 1, \, 2, \, \cdots)$ を

$$
\begin{align}
z_{1} = 1, \, z_{n+1} = (3+4i) z_{n} + 1
\end{align}
$$

によって定める。ただし $i$ は虚数単位である。

(1) すべての自然数 $n$ について

$$
\begin{align}
\frac{3 \times 5^{n-1}}{4} < \left| z_{n} \right| < \frac{5^{n}}{4}
\end{align}
$$

が成り立つことを示せ。

(2) 実数 $r > 0$ に対して，$\left| z_{n} \right| \leqq r$ を満たす $z_{n}$ の個数を $f(r)$ とおく。このとき，$\displaystyle\lim_{n \to \infty} \displaystyle\frac{f(r)}{\log r}$ を求めよ。

1999年度 東大 理系数学 第2問

---

問 題 1 の 解 答

(1)

問題文の不等式を $( \ast )_{n}$ とする。$\left| z_{1} \right| = 1$ より $( \ast )_{1}$ は成り立つ。そこで，$n \geqq 2$ での $( \ast )_{n}$ の成立を，これの十分条件である

$$
\begin{align}
\frac{3 \times 5^{n-1}}{4} + \frac{1}{4} < \left| z_{n} \right| < \frac{5^{n}}{4} - \frac{1}{4} \quad \cdots (\diamondsuit)_{n}
\end{align}
$$

の証明により示す。

まず $z_{2} = (3+4i)\cdot 1 + 1 = 4 + 4i$ より $\left| z_{2} \right| = 4 \sqrt{2}$ であり，$\displaystyle\frac{3 \times 5}{4} + \displaystyle\frac{1}{4} = 4 < 4 \sqrt{2}, \, \displaystyle\frac{5^2}{4} - \displaystyle\frac{1}{4} = 6 > 4 \sqrt{2}$ より $(\diamondsuit)_{2}$ がいえる。

$2$ 以上の自然数 $k$ に対し，$( \diamondsuit )_{k}$ を仮定する。$\left| (3+4i) z_{k} \right| = \left| 3+4i \right| \cdot \left| z_{k} \right| = 5 \left| z_{k} \right|$ であり，$(\diamondsuit)_{k}$ の各辺を $5$ 倍することで

$$
\begin{align}
\frac{3 \times 5^{k}}{4} + \frac{5}{4} < \left| (3 + 4i) z_{k} \right| < \frac{5^{k+1}}{4} - \frac{5}{4}
\end{align}
$$

を得る。一般に複素数 $w_{1}, \, w_{2}$ に対して $| w_{1} | - | w_{2} | \leqq | w_{1} + w_{2} | \leqq |w_{1}| + |w_{2}| $ が成り立つため，

$$
\begin{align}
\frac{3 \times 5^{k}}{4} + \frac{5}{4} - 1 < \left| (3 + 4i) z_{k} + 1 \right| < \frac{5^{k+1}}{4} - \frac{5}{4} + 1
\end{align}
$$

となり，これを整理することで

$$
\begin{align}
\frac{3 \times 5^{k}}{4} + \frac{1}{4} < \left| z_{k+1} \right| < \frac{5^{k+1}}{4} - \frac{1}{4}
\end{align}
$$

となり，$(\diamondsuit)_{k+1}$ がいえる。

以上より $2$ 以上の自然数 $n$ に対し $(\diamondsuit)_{n}$ がいえ，これは $(\ast)_{n}$ の十分条件であり，また $(\ast)_{1}$ は成り立つのだから，任意の自然数 $n$ に対して $(\ast)_{n}$ が成り立つ。■

(2)

実数 $r \geqq \displaystyle\frac{5}{4}$ に対し，

$$
\begin{align}
\frac{5^{N(r)}}{4} \leqq r < \frac{5^{N(r)}}{4}
\end{align}
$$

となる $N(r) \in \mathbb{N}$ がただ 1 つ存在する。このとき

$$
\begin{align}
\begin{cases}
r \geqq \dfrac{5^{N(r)}}{4} > \left| z_{N(r)} \right| > \dfrac{3 \times 5^{N(r) - 1}}{4} > \dfrac{5^{N(r)}-1}{4} > \left| z_{N(r) - 1} \right| > \cdots \\
r < \dfrac{5^{N(r)+1}}{4} < \dfrac{3 \times 5^{N(r)+1}}{4} < \left| z_{N(r) + 2} \right|
\end{cases}
\end{align}
$$

より $N(r) \leqq f(r) \leqq N(r) + 1$ が成り立つ。また，$N(r)$ の条件式の対数をとることで

$$
\begin{align}
N(r) \log 5 - \log 4 \leqq \log r \leqq \left( N(r) + 1 \right) \log 5 - \log 4
\end{align}
$$

となるから，

$$
\begin{align}
\frac{N(r)}{\left( N(r) + 1 \right) \log 5 - \log 4} \leqq f(r) \leqq \frac{N(r) + 1}{N(r) \log 5 - \log 4}
\end{align}
$$

が成り立つ。$r \to \infty$ のとき $N(r) \to \infty$ であり，

$$
\begin{align}
&{} \hspace{5mm} \lim_{N(r) \to \infty} \frac{N(r)}{\left( N(r) + 1 \right) \log 5 - \log 4} \\
&= \lim_{N(r) \to \infty} \frac{1}{\left( 1 + \dfrac{1}{N(r)} \right) \log 5 - \dfrac{1}{N(r)} \log 4} = \dfrac{1}{\log 5}\\
&{} \hspace{5mm} \lim_{N(r) \to \infty} \frac{N(r) + 1}{N(r) \log 5 - \log 4} \\
&= \lim_{N(r) \to \infty} \frac{1 + \dfrac{1}{N(r)}}{\log 5 - \dfrac{1}{N(r)} \log 4} = \dfrac{1}{\log 5}
\end{align}
$$

なので，$\displaystyle\lim_{N(r) \to \infty} \dfrac{f(r)}{\log r} = \dfrac{1}{\log 5}$ がいえる。

以上より，$\displaystyle\lim_{r \to \infty} \dfrac{f(r)}{\log r} = \dfrac{1}{\log 5}$ となる。

---

問 題 1 の ポ イ ン ト ・ 補 足

• 漸化式にある "$+1$" がなんとも邪魔で，(1) の証明は簡単ではありません。これをどう乗り越えるかがこの問題の最大の山場といえるでしょう。複素数の三角不等式を用いると，不等式の両側が 1 ずつ大きくなってしまうため，$5$ 倍して $1$ 足すと同じ形になるよう，あえて不等式の幅を $\dfrac{1}{4}$ ずつ狭めたものを証明するという方針をとりました。
• (1) ができれば (2) はさほど難しくありません。ただし，絶対値が $r$ より小さい $z_{n}$ の個数を正確に求めることにこだわると面倒です。1, 2 個のブレは極限の計算に影響しないので，解説のようにおおらかに考えることで，スムーズに結論を出せます。(評価を厳しくする必要がないという話であって，評価自体は論理的に行うことに注意しましょう。)

---

問 題 2

(1) 実数 $x$ が $-1 < x < 1, \, x \neq 0$ をみたすとき，次の不等式を示せ。

$$
\begin{align}
(1-x)^{1 - \frac{1}{x}} < (1 + x)^{1 + \frac{1}{x}}
\end{align}
$$

(2) 次の不等式を示せ。

$$
\begin{align}
0.9999^{101} < 0.99 < 0.9999^{100}
\end{align}
$$

2009年度 東大 理系数学 第5問

---

問 題 2 の 解 答

(1)

$$
\begin{align}
&{} (1-x)^{1 - \frac{1}{x}} < (1 + x)^{1 + \frac{1}{x}} \quad (-1 < x < 1) \quad \cdots (\ast)\\
&\Leftrightarrow \left( 1 - \frac{1}{x} \right) \log (1-x) < \frac{1}{x} \log ( 1 + x) \\
&\Leftrightarrow
\begin{cases}
\log(1+x) + (1-x) \log (1-x) > 0 \quad (0< x < 1) \\
\log (1+x) + (1-x) \log (1-x) < 0 \quad (-1 < x < 0)
\end{cases}
\end{align}
$$

であるため，最後の不等式を示すこととする。

$f(x) := \log (1+x) + (1-x) \log (1-x) \quad (-1 < x < 1)$ とすると，

$$
\begin{align}
f'(x) &= \frac{1}{1+x} - \log (1-x) + (1-x) \cdot \frac{-1}{1-x} \\
&= \frac{1}{1+x} - \log (1-x) - 1 \\
f''(x) &= - \frac{1}{(1+x)^2} - \frac{-1}{1-x} = \frac{x(x+3)}{(1+x)^2 (1-x)}
\end{align}
$$

であるため，関数 $f(x)$ やその導関数の増減は次のとおり。

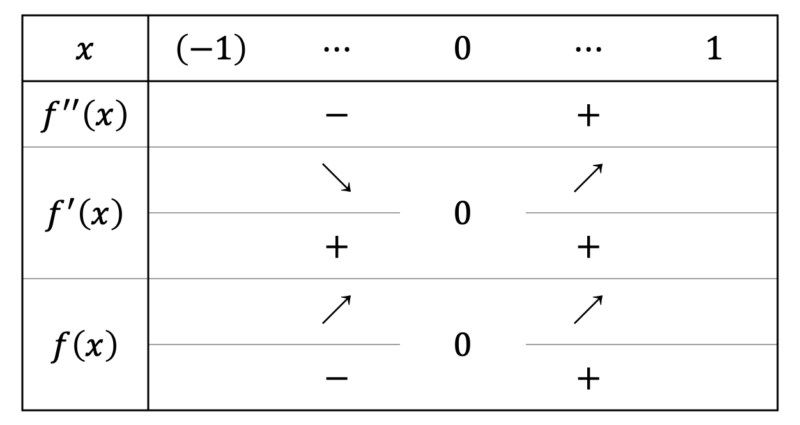
よって $-1<x<0$ で $f(x) < 0$，$0<x<1$ で $f(x) > 0$ だから，$(\ast)$ が成り立つ。■

(2)

$(\ast)$ で $x = 0.01$ とすると $0.99^{-99} < 1.01^{100}$ となり，この両辺に $0.99^{100}$ をかけることで $0.99 < 0.9999^{100}$ を得る。また $(\ast)$ で $x = -0.01$ とすると $1.01^{101} < 0.99^{-100}$ となり，両辺に $0.99^{101}$ をかけることで $0.9999^{101} < 0.99$ を得る。以上より $0.9999^{101} < 0.99 < 0.9999^{100}$ が成り立つ。■

---

問 題 2 の ポ イ ン ト ・ 補 足

• (1) の不等式は，まず両辺の対数を考え，たとえば解説のように 2 回の導関数を計算することにより示せます。対数を考えるとき，両辺に $x$ をかけて式を単純にするのは有効な作業ですが，$x$ の符号により不等号の向きが逆になることに注意しましょう。
• (2) も悩む人が多いでしょうが，0.9999 という数を合わせるのではなく指数を合わせることを考えると，$x = \pm 0.01$ を代入するという発想に自然に到達します。$0.9999 = 0.99 \times 1.01$ であることに気づけるかどうかも分かれ目かもしれません。
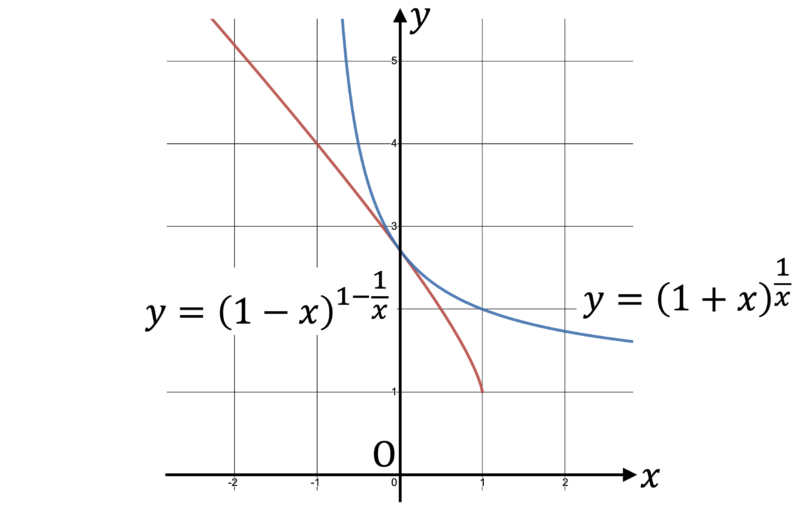
• 2 つの関数 $y = (1-x)^{1-\frac{1}{x}}, \, y = (1+x)^{\frac{1}{x}}$ のグラフを図示すると次のようになります。

---

ま と め

このように，指数・対数の問題は他分野との融合で出題されることが多いです。
特に不等式の証明問題は 2016 年度にも出題されているため，ぜひ対策をしておきたいところですね。
ぱっと見で解法がわかる程度の難易度は期待できず，問題演習の経験をもとに試行錯誤するステップが多くの場合必要となります。
普段問題演習をするときは，わからなかったらすぐに解説を読むのではなく，粘り強く考える練習もしましょう。