【東大数学分野別解説】#11 二次関数との融合が頻出の "三角関数"

三角関数は，文系数学・理系数学共に頻出です。
三角関数単体でというよりは，二次関数との融合で出題されることが多い印象です。(これはあくまで林個人の印象)
そこで今回は，二次関数と関係する三角関数の問題をご紹介します。

問 題 1

$2$ つの放物線

$$
\begin{align}
y &= 2 \sqrt{3} \left( x - \cos \theta \right)^2 + \sin \theta \\
y &= - 2 \sqrt{3} \left( x + \cos \theta \right)^2 - \sin \theta
\end{align}
$$

が相異なる $2$ 点で交わるような一般角 $\theta$ の範囲を求めよ。

2002年度 東京大学 理系数学 第1問 (文系でもほぼ同じものが出題されました。)

---

問 題 1 の 解 答

2 式の右辺が等しいとき $2 \sqrt{3} \left( x - \cos \theta \right)^2 + \sin \theta = - 2 \sqrt{3} \left( x + \cos \theta \right)^2 - \sin \theta$ が成り立ち，これは $2 \sqrt{3} x^2 + 2 \sqrt{3} \cos^2 \theta + \sin \theta = 0$ と同値である。この方程式の解がどのような値でも，それと問題文の 2 式より $y$ の値が定まるため，問題文の条件は "$x$ の 2 次方程式

$$
\begin{align}
2 \sqrt{3} x^2 + 2 \sqrt{3} \cos^2 \theta + \sin \theta = 0
\end{align}
$$

が相異なる 2 実解をもつ" ことと必要十分である。この条件を整理すると

$$
\begin{align}
2 \sqrt{3} \cos^2 \theta + \sin \theta &< 0 \\
2 \sqrt{3} \left( 1 - \sin^2 \theta \right) + \sin \theta &< 0 \\
2 \sqrt{3} \sin^2 \theta - \sin \theta - 2 \sqrt{3} &> 0 \\
\left( 2 \sin \theta + \sqrt{3} \right) \left( \sqrt{3} \sin \theta - 2 \right) &> 0\\
\sin \theta < - \frac{\sqrt{3}}{2} \, {\rm または} \, \sin \theta &> \frac{2}{\sqrt{3}}
\end{align}
$$

となり，$\sin \theta$ がそもそも $-1$ 以上 $1$ 以下の値しかとりえないことを踏まえると $\left( -1 \leqq \right) \sin \theta < \displaystyle\frac{\sqrt{3}}{2}$ のみとなる。これをみたすのは

$$
\begin{align}
\underline{\left( \frac{4}{3} + 2k \right) \pi < \theta < \left( \frac{5}{3} + 2k \right) \pi \quad \left( k \, {\rm は整数} \right)}
\end{align}
$$

となる。

---

問 題 1 の ポ イ ン ト ・ 補 足

大変シンプルな問題でした。実際の試験では確実に正解したいところです。
このように，方程式や不等式の中で (定数として) 三角関数が登場する問題は，他にもたとえば 2006 年度の文系数学第4問で登場しています。

---

問 題 2

実数 $a, \, b$ に対して

$$
\begin{align}
f(\theta) = \cos 3\theta + a \cos 2\theta + b \cos \theta
\end{align}
$$

とし，$0 < \theta < \pi$ で定義された関数

$$
\begin{align}
g(\theta) = \frac{f(\theta) - f(0)}{\cos \theta - 1}
\end{align}
$$

を考える。

(1) $f(\theta)$ と $g(\theta)$ を $x = \cos \theta$ の整式で表せ。

(2) $g(\theta)$ が $0 < \theta < \pi$ の範囲で最小値 $0$ をとるための $a, \, b$ についての条件を求めよ。また，条件をみたす点 $(a, \, b)$ が描く図形を座標平面上に図示せよ。

2017年度 東大 理系数学 第1問

---

問 題 2 の 解 答

(1)

$2$ 倍角・$3$ 倍角の公式より，$f(\theta)$ は

$$
\begin{align}
f(\theta) &= \cos 3 \theta + a \cos 2 \theta + b \cos \theta \\
&= \left( 4 \cos^3 \theta - 3 \cos \theta \right) + a \left( 2 \cos^2 \theta - 1 \right) + b \cos \theta \\
&= 4 \cos^3 \theta + 2a \cos^2 \theta + (b-3) \cos \theta - a \\
&= \underline{4x^3 + 2ax^2 + (b-3) x - a}
\end{align}
$$

となる。また，$\theta = 0$ のとき $\cos \theta = 1$ であることに注意すると

$$
\begin{align}
g(\theta) &= \frac{f(\theta) - f(0)}{\cos \theta - 1} \\
&= \frac{4x^3 + 2ax^2 + (b-3) x - a - \left\{ 4 + 2a + (b-3) - a \right\}}{x - 1} \\
&= \frac{4(x^3 - 1) + 2a (x^2 - 1) + (b-3)(x-1)}{x-1} \\
&= 4(x^2 + x + 1) + 2a ( x + 1) + (b-3) \\
&= \underline{4x^2 + 2(a+2)x + (2a + b + 1)}
\end{align}
$$

と計算できる。

(2)

$G(x) := 4x^2 + 2(a+2)x + (2a + b + 1)$ と定める。このとき

$$
\begin{align}
G(x) &= 4x^2 + a(a+2) x + (2a + b + 1) \\
&= 4 \left( x + \frac{a+2}{4} \right)^2 + (2a + b + 1) - \frac{1}{4} (a+2)^2 \\
&= 4 \left( x + \frac{a+2}{4} \right)^2 + \left( - \frac{1}{4} a^2 + a + b \right)
\end{align}
$$

であるため，問題文の条件は "$x$ の関数 $G(x)$ が $-1 < x < 1$ の範囲で最小値 0 をとる" ことと必要十分である。

放物線 $y = G(x)$ の軸は直線 $x = - \displaystyle\frac{a+2}{4}$ であるため，求める条件は

$$
\begin{align}
\begin{cases}
-1 < - \displaystyle\frac{a+2}{4} < 1 \\
- \displaystyle\frac{1}{4} a^2 + a + b = 0
\end{cases}
\Leftrightarrow
\underline{
\begin{cases}
-6 < a < 2\\
b = \displaystyle\frac{1}{4} a^2 - a
\end{cases}
}
\end{align}
$$

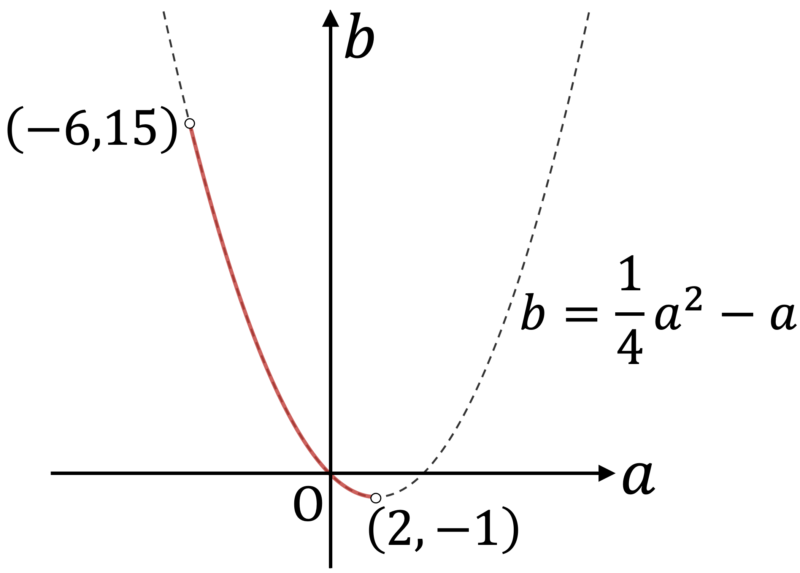
である。これを図示すると次のようになる。(赤線部，両端の点を除く。)

---

問 題 2 の ポ イ ン ト ・ 補 足

問題文の見た目はやや複雑ですが，実際に手を動かしてみるとただの 2 次関数の問題となります。
一般に，正の整数 $n$ に対し多項式 $x^{n} - 1$ は多項式 $x - 1$ で割り切れます。これは経験的に知っている人が多いと思いますが，様々な分野で時折この割り算が登場するので覚えておくとよいでしょう。
平易な問題ではありましたが，$\theta$ の変域を考えているのか $x$ の変域を考えているのかは混同しないように注意！

---

ま と め

あくまで林の個人的な印象ですが，三角関数は二次方程式や二次不等式との融合で出題されることが多いです。
京都大学の数学にも三角関数の問題はいくつかあるので，必要に応じてそれらも演習してみましょう。(1993年度文系数学第1問, 2012年度文系数学第5問, 2008年度文系数学第4問，2004年度文系数学第1問 など)