【東大数学分野別解説】#09 計算を工夫する "整式の微積分"
連載:東大数学分野別解説
2022.02.01
今回もテーマは "整式" ですが,今回は特に微分・積分を伴うものを扱います。
理系でも時折出題はありますが,特に文系の受験生にとって重要な内容です!
問 題 1
$a$ は $0$ でない実数とする。関数
$f(x) = (3x^{2} - 4) \left( x - a + \displaystyle\frac{1}{a} \right)$
の極大値と極小値の差が最小となる $a$ の値を求めよ。
1998年 東大 文理共通問題
問 題 1 の 解 答
$f$ の導関数は
$$
\begin{align}
f'(x) &= \left\{ 3x^{3} + 3 \left( -a + \displaystyle\frac{1}{a} \right) x^{2} \right. \\
&{} \hspace{10mm} \left. - 4x - 4 \left( -a + \displaystyle\frac{1}{a} \right) \right\}' \\
&= 9x^2 + 6 \left( -a + \displaystyle\frac{1}{a} \right) x -4 \\
&= \left( 3x - 2a \right) \left( 3x + \displaystyle\frac{2}{a} \right)
\end{align}
$$
であるため,$f'(x) = 0 \Leftrightarrow x = \displaystyle\frac{2}{3} a, \, - \displaystyle\frac{2}{3a}$ となる。なお,$a \neq 0$ のときこれらは異符号であるため,等しくなることはない。よって関数 $f$ には極大値・極小値が存在し,それらの差は
$$
\begin{align}
&{} \hspace{8mm} \left| f \left( - \displaystyle\frac{2}{3a} \right) - f \left( \displaystyle\frac{2}{3} a \right) \right| \\
&= \left| \left( \displaystyle\frac{4}{3a^2} - 4 \right) \left( -a + \displaystyle\frac{1}{3a} \right) - \left( \displaystyle\frac{4}{3} a^2 - 4 \right) \left( - \displaystyle\frac{1}{3} a + \displaystyle\frac{1}{a} \right) \right| \\
&= \left| \left( 4a - \displaystyle\frac{8}{3a} + \displaystyle\frac{4}{9a^3} \right) - \left( - \displaystyle\frac{4}{9} a^{3} + \displaystyle\frac{8}{3} a - \displaystyle\frac{4}{a} \right) \right| \\
&= \left| \displaystyle\frac{4}{9} a^3 + \displaystyle\frac{4}{3} a + \displaystyle\frac{4}{3a} + \displaystyle\frac{4}{9a^3} \right| \\
&= \left| \displaystyle\frac{4}{9a^3} \left( a^{6} + 3a^{4} + 3a^{2} + 1 \right) \right| \\
&= \left| \displaystyle\frac{4}{9a^3} \left( a^{2} + 1 \right)^3 \right| \\
&= \displaystyle\frac{4}{9} \left( |a| + \displaystyle\frac{1}{|a|} \right)^3
\end{align}
$$
である。ここで相加平均・相乗平均の不等式より
$$
\begin{align}
|a| + \displaystyle\frac{1}{|a|} \geqq 2 \sqrt{|a| \cdot \displaystyle\frac{1}{|a|}} = 2
\end{align}
$$
が成り立ち,等号は $|a| = \displaystyle\frac{1}{|a|}$ つまり $a = \pm 1$ のときに成り立つ。$\left( |a| + \displaystyle\frac{1}{|a|} \right)^3$ の増減と $|a| + \displaystyle\frac{1}{|a|}$ の増減は一致するため,$f$ の極大値・極小値の差が最小となるのも $\underline{a = \pm 1}$ のときである。
問 題 1 の ポ イ ン ト ・ 補 足
東大の入試問題にしては大変シンプルですが,時折こうした問題も出題されます。
極大点・極小点の $x$ 座標の組を求めたあと,どちらが極大点でどちらが極小点になるかで場合分けをする人も多いでしょうし,それも全く問題ありません。ただ,いま考えているのはあくまで "差" なので,絶対値を考えることで解説のように統一して記述することができます。時間短縮にもなりますし答案のスペースも節約できるので,実際の試験でもこのような工夫ができるといいですね。(決して飛躍的な発想ではないと思います。)
問 題 2
座標平面上の放物線 $C$ を $y = x^{2} + 1$ と定める。$s, \, t$ は実数とし $t < 0$ を満たすとする。点 $(s, \, t)$ から放物線 $C$ へ引いた接線を $l_{1}, \, l_{2}$ とする。
(1) $l_{1}, \, l_{2}$ の方程式を求めよ。
(2) $a$ を正の実数とする。放物線 $C$ と直線 $l_{1}, \, l_{2}$ で囲まれる領域の面積が $a$ となる $(s, \, t)$ を全て求めよ。
2012年 東大 文系数学 第4問
問 題 2 の 解 答
(1)
$\left( x^{2} + 1 \right)' = 2x$ より,放物線 $C$ 上の点 $(u, \, u^{2} + 1)$ における $C$ の接線の方程式は
$$
\begin{align}
y - (u^2 + 1) = 2u(x-u) \quad \left( \Leftrightarrow y = 2ux + (- u^{2} + 1) \right)
\end{align}
$$
となる。これが点 $(s, \, t)$ を通るとき
$$
\begin{align}
t = 2us + (-u^2 + 1) \hspace{10mm} \therefore u = s \pm \sqrt{s^2 - t + 1}
\end{align}
$$
となる ($s^{2} - t + 1 > 0$ となることに注意)。複号の選び方に応じてこれらを $u_{\pm}$ とすると,$l_{1}, \, l_{2}$ の方程式は
$$
\begin{align}
y = 2 u_{\pm} x + \left( - u_{\pm}^{2} + 1 \right) \quad \left( {\rm ただし} \, u_{\pm} = s \pm \sqrt{s^2 - t + 1} \right)
\end{align}
$$
と求められる。(2 直線の方程式は順不同だが,$u_{+}$ に対応する方を $l_{2}$,$u_{-}$ に対応する方を $l_{1}$ とする。)
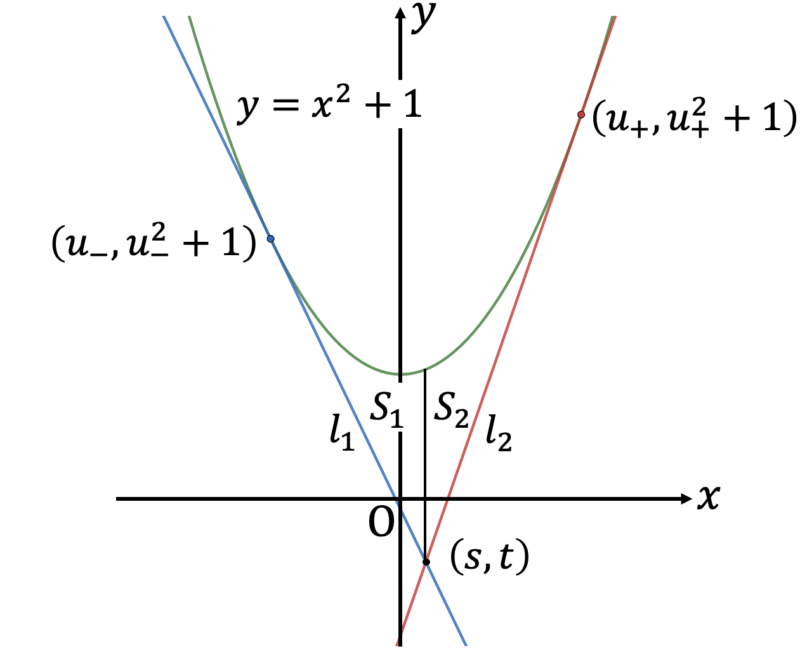
(2)
放物線 $C$ と直線 $l_{1}$,そして直線 $x = s$ で囲まれる領域の面積を $S_{1}$ とする。また,放物線 $C$ と直線 $l_{2}$,そして直線 $x = s$ で囲まれる領域の面積を $S_{2}$ とする。このとき
$$
\begin{align}
S_{1} &= \int_{u_{-}}^{s} \left\{ (x^2 + 1) - \left( 2 u_{-} x + (-u_{-}^{2} + 1 ) \right) \right\} \, dx \\
&= \int_{u_{-}}^{s} \left( x - u_{-} \right)^2 \, dx \\
&= \left[ \displaystyle\frac{1}{3} \left( x - u_{-} \right)^3 \right]_{u_{-}}^{s} = \displaystyle\frac{1}{3} \left( s - u_{-} \right)^3 \\
&= \displaystyle\frac{1}{3} \sqrt{s^{2} - t + 1}^3
\end{align}
$$
$$
\begin{align}
S_{2} &= \int_{s}^{u_{+}} \left\{ (x^2 + 1) - \left( 2 u_{+} x + (-u_{+}^{2} + 1 ) \right) \right\} \, dx \\
&= \int_{s}^{u_{+}} \left( x - u_{+} \right)^2 \, dx \\
&= \left[ \displaystyle\frac{1}{3} \left( x - u_{+} \right)^3 \right]_{s}^{u_{+}} = \displaystyle\frac{1}{3} \left( u_{+} - s \right)^3 \\
&= \displaystyle\frac{1}{3} \sqrt{s^{2} - t + 1}^3
\end{align}
$$
であるため,放物線 $C$ と直線 $l_{1}, \, l_{2}$ で囲まれる図形の面積は
$$
\begin{align}
S = S_{1} + S_{2} = \displaystyle\frac{2}{3} \sqrt{s^2 - t + 1}^3
\end{align}
$$
と計算できる。これが $a$ となるとき,
$$
\begin{align}
\displaystyle\frac{2}{3} \sqrt{s^2 - t + 1}^3 &= a \\
\therefore s^{2} - t + 1 &= \left( \displaystyle\frac{3}{2} a \right)^{\frac{2}{3}} \quad \left( \Leftrightarrow t = s^2 + 1 - \left( \displaystyle\frac{3}{2} a \right)^{\frac{2}{3}} \right)
\end{align}
$$
であるが,$t < 0$ であることに注意すると,ある実数 $s$ が存在して $s^2 + 1 - \left( \displaystyle\frac{3}{2} a \right)^{\frac{2}{3}} < 0$ が成り立つ必要がある。その必要十分条件は
$$
\begin{align}
1 - \left( \displaystyle\frac{3}{2} a \right)^{\frac{2}{3}} < 0 \quad \Leftrightarrow \quad a > \displaystyle\frac{2}{3}
\end{align}
$$
である。以上より,条件を満たす $(s, \, t)$ は
$$
\begin{align}
\begin{cases}
a > \displaystyle\frac{2}{3} \, {\rm のとき} \quad t = s^2 + 1 - \left( \displaystyle\frac{3}{2} a \right)^{\frac{2}{3}} \, {\rm かつ} \\
\hspace{50mm} \, t < 0 \, {\rm を満たす} \, (s, \, t) \, {\rm の組全体} \\
\left( 0 < \right) \, a \leqq \displaystyle\frac{2}{3} \, {\rm のとき} \quad {\rm 条件を満たす} \, (s, \, t) \, {\rm は存在しない}
\end{cases}
\end{align}
$$
と求められる。■
問 題 2 の ポ イ ン ト ・ 補 足
放物線とその接線で囲まれる図形の面積は,共通テストから東大の二次試験までさまざまなところで登場します。
接点からの $x$ 座標のズレの $3$ 乗で図形の面積が決まるのがポイントですね。
また,本問では $S_{1} = S_{2}$ が成り立ちますが,これは 1 点から放物線に引いた 2 本の接線について一般的に成り立つ性質です。これも知っておくと,共通テストでラクに計算できたり検算に使えたりすることでしょう。
なお,厳密には 数学II で学習する範囲ではないようですが,
$$
\begin{align}
\int (x - a)^{n} = \displaystyle\frac{1}{n+1} \left( x - a \right)^{n+1} + {\rm const.} \quad (n : \, {\rm 正の整数})
\end{align}
$$
という積分公式は覚えておくとよいでしょう。これを用いることで効率よく面積計算ができる場面が結構たくさんあります。
問 題 3
2 次以下の整式 $f(x) = ax^{2} + bx + c$ に対し
$$
\begin{align}
S = \displaystyle\int_{0}^{2} \left| f'(x) \right| \, dx
\end{align}
$$を考える。
(1) $f(0) = 0, \, f(2) = 2$ のとき $S$ を $a$ の関数として表せ。
(2) $f(0) = 0, \, f(2) = 2$ をみたしながら $f$ が変化するとき,$S$ の最小値を求めよ。
2009年 東大 文系数学 第4問
問 題 3 の 解 答
(1)
$f(0) = 0$ より $c = 0$ となる。また,$f(2) = 2$ より $4a + 2b = 2$ つまり $b = -2a + 1$ もいえる。よって $f(x) = ax^2 + (-2a+1)x$ が成り立つ。これより $f'(x) = 2ax + (-2a + 1)$ となる。
$a = 0$ のときつねに $f'(x) = 1$ より $S = 2$ となる。
次に $a \neq 0$ のときを考える。$f'(x) = 0 \Leftrightarrow x = 1 - \displaystyle\frac{1}{2a}$ である。この値が $0 < x < 2$ の範囲に入るのは $|a| > \displaystyle\frac{1}{2}$ のときである。
$f'(x)$ が一次関数であるため,積分が三角形の面積として計算できることに注意すると,$|a| > \displaystyle\frac{1}{2}$ のときは
$$
\begin{align}
S &= \left| \displaystyle\int_{0}^{1 - \frac{1}{2a}} f'(x) \, dx \right| + \left| \displaystyle\int_{1 - \frac{1}{2a}}^{2} f'(x) \, dx \right| \\
&= \displaystyle\frac{1}{2} \left( 1 - \frac{1}{2a} \right) \left| f'(0) \right| + \displaystyle\frac{1}{2} \left( 2 - \left( 1 - \frac{1}{2a} \right) \right) \left| f'(2) \right| \\
&= \displaystyle\frac{1}{2} \left( 1 - \frac{1}{2a} \right) \left| -2a+1 \right| + \displaystyle\frac{1}{2} \left( 1 + \frac{1}{2a} \right) \left| 2a+1 \right| \\
&= \displaystyle\frac{ (2a-1) \left| -2a+1 \right|}{4a} + \displaystyle\frac{ (2a+1) \left| 2a+1 \right|}{4a} \\
&= \displaystyle\frac{ (2a-1)^2}{4|a|} + \displaystyle\frac{ (2a+1)^2 }{4|a|} \\
&= \displaystyle\frac{8a^2 + 2}{4|a|} \\
&= 2|a| + \displaystyle\frac{1}{2|a|}
\end{align}
$$
と計算できる。
$(0<) \, |a| < \displaystyle\frac{1}{2}$ のときは,直線 $y = f'(x)$ が $0 < x < 2$ の範囲で $x$ 軸と交わらない。またつねに $f'(1) = 1$ であるから,$f'(0) \geqq 0, \, f'(2) \geqq 0$ が成り立ち,$S$ は台形の面積として
$$
\begin{align}
S &= \displaystyle\frac{1}{2} \cdot \left\{ f'(0) + f'(2) \right\} \cdot 2 = 2 \quad ( \because f(0) = 0, \, f(2) = 2 )
\end{align}
$$
と計算できる ($a = 0$ のときもこれに該当する)。
以上より
$$
\begin{align}
S =
\begin{cases}
2|a| + \displaystyle\frac{1}{2|a|} \quad \left( |a| > \displaystyle\frac{1}{2} \, {\rm のとき} \right) \\
2 \quad \left( a \leqq \displaystyle\frac{1}{2} \, {\rm のとき} \right)
\end{cases}
\end{align}
$$
と計算できる。
(2)
$|a| > \displaystyle\frac{1}{2}$ のとき,相加平均・相乗平均の不等式より
$$
\begin{align}
2|a| + \frac{1}{2|a|} \geqq 2 \sqrt{2|a| \cdot \frac{1}{2|a|}} = 2
\end{align}
$$
が成り立つ。また $a \leqq \displaystyle\frac{1}{2}$ のとき $S = 2$ である。よって $S$ の最小値は 2 である。
問 題 3 の ポ イ ン ト ・ 補 足
絶対値つきの積分なので面倒に思えますが,$f'(x)$ がたかだか一次関数であるため,三角形や台形の面積を利用して思いのほか簡単に計算できます。
答案でも図を添えておいた方が,積分の計算過程が理解しやすいかもしれませんね。
解説では $a$ の符号による場合分けをせずに統一して記述しましたが,逆にこうした書き方だと混乱してしまうという人は,場合分けしてももちろん OK です。
ま と め
今回は,整式の問題の中でも微分・積分に関連するものをピックアップしました。
特に 問題3 のような定積分の最大値・最小値問題は,文系入試で頻出の問題の一つです。計算量も少なくない分野なので,文系受験生もたくさん問題演習をしておきましょう。
理系においては最重要というほどではないですが,多項式の微分・積分自体はさまざまな問題で部分的に登場するので,ミスなく正確に計算できるよう鍛錬しましょう。