理系のための東大文系数学 2008年 第3問（条件をみたす点の軌跡）

今回は「図形と方程式」の単元から 1 題ピックアップしました。
解法選択も一つの分岐点ですが，どのみちそれなりに煩雑な計算が待っています。
しんどい問題ですが，理系受験生であれば正答に辿り着いてほしいところです。

問 題

座標平面上の 3 点 ${\rm A}(1, 0)$, ${\rm B}(-1, 0)$, ${\rm C}(0, -1)$ に対し，

$\angle {\rm APC} = \angle {\rm BPC}$

をみたす点 ${\rm P}$ の軌跡を求めよ。ただし ${\rm P \neq A, B, C}$ とする。

2008年 東京大学 前期二次試験 数学（文科） 第3問

解 答

${\rm P}(x, y)$ とおき，$x$ と $y$ のみたすべき関係式を求める。まず ${\rm P \neq A, B, C}$ より $(x, y) \neq (\pm 1, 0), \, (0, -1)$ である。問題文の条件式は

$$
\begin{align}
\angle {\rm APC} = \angle {\rm BPC} &\Leftrightarrow \cos \angle {\rm APC} = \cos \angle {\rm BPC}\\
&\Leftrightarrow \frac{\overrightarrow{{\rm PA}} \cdot \overrightarrow{{\rm PC}}}{\vert \overrightarrow{{\rm PA}} \vert \vert \overrightarrow{{\rm PC}} \vert}=\frac{\overrightarrow{{\rm PB}} \cdot \overrightarrow{{\rm PC}}}{\vert \overrightarrow{{\rm PB}} \vert \vert \overrightarrow{{\rm PC}} \vert} \\
&\Leftrightarrow \left( \overrightarrow{{\rm PA}} \cdot \overrightarrow{{\rm PC}} \right) \vert \overrightarrow{{\rm PB}} \vert =\left( \overrightarrow{{\rm PB}} \cdot \overrightarrow{{\rm PC}} \right) \vert \overrightarrow{{\rm PA}} \vert
\end{align}
$$

と言い換えられる（この最後の式を (*) とする）。ここで

$$
\begin{align}
\overrightarrow{{\rm PA}} = (1-x, -y), \, \overrightarrow{{\rm PB}}=(-x-1,-y), \, \overrightarrow{{\rm PC}}=(-x, -1-y)
\end{align}
$$

を代入して整理すれば，

$$
\begin{align}
(*) &\Leftrightarrow (x^2-x+y^2+y) \sqrt{(x+1)^2+y^2 } \\
&{} \hspace{15mm} =(x^2+x+y^2+y) \sqrt{(x-1)^2+y^2 } \\
&\Leftrightarrow
\begin{cases}
x^2-x+y^2+y \, {\rm と} \, x^2+x+y^2+y \, {\rm が異符号でない} \\
xy(x^2+y^2-1)=0 \\
\end{cases}\\
&\Leftrightarrow
\begin{cases}
\left\{ \left( x - \displaystyle\frac{1}{2} \right)^2 + \left( y + \displaystyle\frac{1}{2} \right)^2 - \displaystyle\frac{1}{2} \right\} \\
\hspace{10mm} \cdot \left\{ \left( x + \displaystyle\frac{1}{2} \right)^2 + \left( y - \displaystyle\frac{1}{2} \right)^2 - \displaystyle\frac{1}{2} \right\} \geqq 0 \\
x = 0 \, {\rm または} \, y = 0 \, {\rm または} x^2 + y^2 = 1 \\
\end{cases}
\end{align}
$$

となる。以上より，条件をみたす点 ${\rm P}(x, y)$ の軌跡は次図の太線部のようになる。ただし点 ${\rm A, B, C}$ を除く。

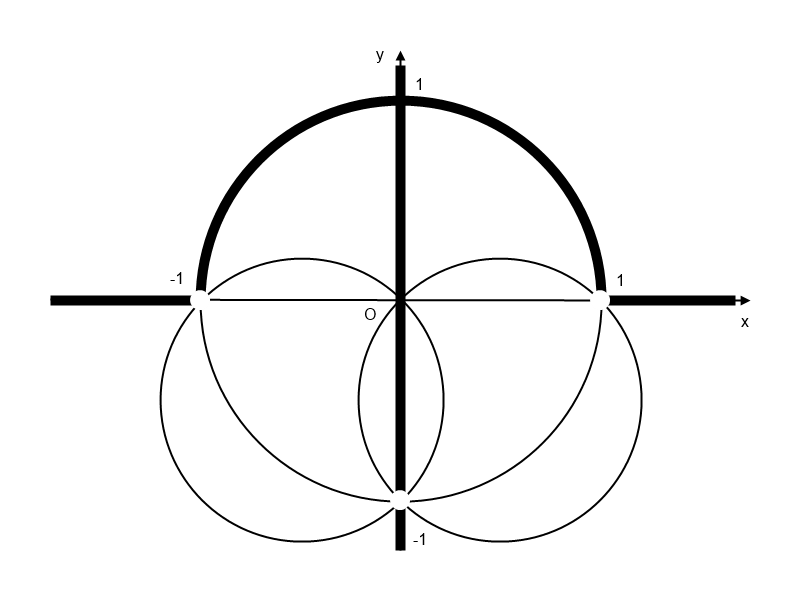
コ メ ン ト

問題文の条件式は至ってシンプルなのですが，点 ${\rm P}$ の座標を $(x, y)$ として条件式をいざ立ててみると，思いの外計算が大変になります。
上の解説では条件式を整理する過程を省いているので，各自で計算してみてください。
想像以上に大変だと思います。

今回の解法は何も工夫をしていないため，すぐに答案作成に取り組むことができます。一方で無策といえば無策であるため，途中計算が大変になりました。
逆に，最初に面倒でもちょっと工夫をすることで，計算式の次数を下げられる解法もあります。
たとえば ${\rm PA} = a, \, {\rm PB} = b, \, {\rm PC} = c$ として $a, \, b, \, c$ を用いて同じように $\cos$ の条件式を立ててみると，早い段階で因数分解された条件式が出てきます。
これにより，式の次数を抑えつつ計算が進められるので多少楽です。

また，意欲ある受験生のみで構いませんが，この問題は複素数平面を用いた解法もあります。
興味のある人はぜひ試してみてください！