理系のための東大文系数学 2020年第2問（数え上げのポイント）

2021.12.03

東大数学の過去問には良問が多いですが，直前にセットで解く用に解かずに取っておく人は少なくありません。ただ，東大模試の問題ももちろん悪くはないのですが，やはりオリジナルの問題は別格です。そこで理系の皆さんは，東大入試で文系数学として出題されたものの中で，文系数学の問題を解いてみるのはいかがでしょうか？出題範囲は数学Ⅰ, A, II, B に限られますが，理系で出されてもおかしくない問題が結構ありますし，仮に出題された場合ちょうど合否を分けるレベルになっていることも珍しくありません。少しでも本番に近い問題を解いて，東大合格に近付きましょう！

東大の場合の数・確率分野と聞くと "確率漸化式" を思い浮かべる受験生が多いかもしれませんが, 実は最近の入試でシンプルな数え上げの問題が出題さています。
というわけで今回は, "数え上げ" の問題を攻略するポイントを解説します。

問題

座標平面上に 8 本の直線
$x = a \quad (a = 1, \, 2, \, 3, \,4 ), \hspace{8mm} y = b \quad (b = 1, \, 2, \, 3, \, 4 )$
がある。以下，16 個の点
$\hspace{8mm} (a, \, b) \quad (a = 1, \,2, \,3, \,4 \quad b = 1, \, 2, \, 3, \, 4)$
から異なる 5 個の点を選ぶことを考える。
(1) 次の条件を満たす 5 個の点の選び方は何通りあるか。
　上の 8 本の直線のうち，選んだ点を 1 個も含まないものがちょうど 2 本ある。
(2) 次の条件を満たす 5 個の点の選び方は何通りあるか。
　上の 8 本の直線は，いずれも選んだ点を少なくとも 1 個含む。
2020年東京大学前期二次試験数学（文科）第2問

解答

$x$ 軸方向を ”横”, $y$ 軸方向を ”縦” とよぶ。

(1)

選んだ点を $1$ 個も含まない直線が $2$ 本あるとき, それらは (a) 平行, (b) 垂直, の $2$ つのいずれか。

(a) ${\bf 2}$ 直線が平行のとき

それら $2$ 直線の選び方は ${}_{4}{{\rm C}}_{2} \times 2 = 12$ 通り。

たとえば, 選んだ点を含まない直線が，上の点線となっている直線であるとする。このとき右の $2 \, {\rm 列} \times 4 \, {\rm 個} = 8 {\rm 個}$ の点から $5$ 個点を選ぶことになる。
ここで, 横に並んだ $2$ 点の組を「段」とよぶこととする。どの実線上にも選ばれる点が少なくとも $1$ 個必要なため, $4$ 段それぞれに少なくとも $1$ 個の選ばれる点が存在し, $1$ つの段のみ $2$ 個が選ばれることとなる。このとき縦の $2$ 直線は必ず選ばれる点を含むから, 上図における点の選び方は ${}_{4}{{\rm C}}_{1} \times 2^{3} = 4 \times 8 = 32$ 通りである。

よって，条件をみたす場合の数は $12 \times 32 = 384$ 通りとなる。

(b) ${\bf 2}$ 直線が垂直のとき

それら $2$ 直線の選び方は $4 \times 4 = 16$ 通り。

選んだ点を $1$ 個も含まない直線が上の点線となっている $2$ 直線であるとする。このとき, 残りの $3 \times 3 = 9$ 個の交点より $5$ 個選ぶが, $6$ 本の直線全てが点を含むことは, $6$ つの行または列のうち, $3$ 点すべてが選ばれないようなものが存在しないことと同じである。そして $9$ 個の点から $5$ 個選ぶとき, $3$ 点すべてが選ばれないような行・列は高々 $1$ つ。したがって, $9$ 個の点から $5$ 個選ぶ方法から $3$ 点すべてが選ばれないような行・列のある選び方を引けばよく, その場合の数は ${}_{9} {{\rm C}}_{5} - 6 \times {}_{6} {{\rm C}}_{5} = 90$ 通りである。

$2$ 直線の選び方 $16$ 通りの各々についてこの議論が成り立つため, 条件をみたす場合の数は $16 \times 90 = 1440$ 通りとなる。

以上より, 条件をみたす点の選び方の総数は $384 + 1440 = \underline{1824}$ 通りである。

(2)

縦 $4$ 本, 横 $4$ 本の直線の交点から $5$ 個選ぶため, 縦の直線の中には $2$ 個の点を含むものがちょうど $1$ つ存在し ($V$ とする), ほかの $3$ 直線は $1$ 点ずつ含む。同様に, 横の直線の中には $2$ 個の点を含むものがちょうど $1$ つあり ($W$ とする), ほかの $3$ 直線は $1$ 点ずつ含む。

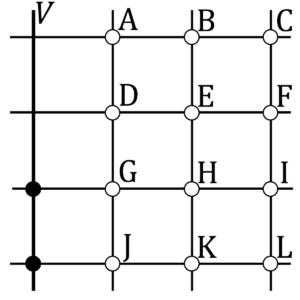
$V$ とそれが含む $2$ 点が上図のようであったとする。このとき, (a) $V, \, W$ の交点が選ばれる, (b) $V, \, W$ の交点が選ばれない, のいずれか。

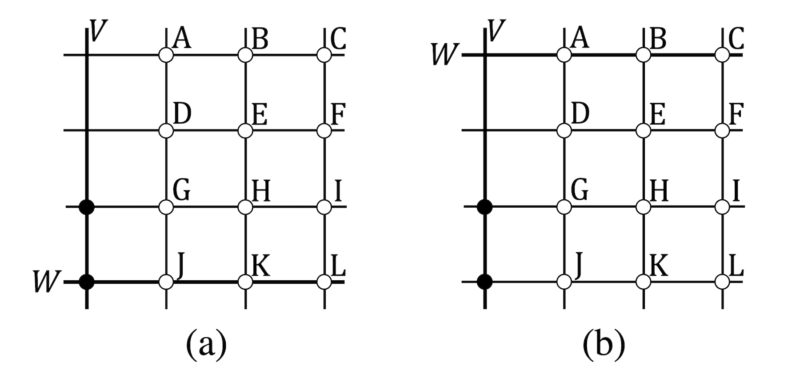
(a) $V$ と $W$ の交点が選ばれる場合

$W$ は上図の位置とする。このとき, $\{ {\rm J}, \, {\rm K}, \, {\rm L} \}$ から $1$ つ, $\{ {\rm A}, \, {\rm B}, \, {\rm C}, \, {\rm D}, \, {\rm E}, \, {\rm F} \}$ から $2$ つ選ぶこととなる。$\{ {\rm J}, \, {\rm K}, \, {\rm L} \}$ からの選び方は $3$ 通りであり, たとえば ${\rm J}$ を選んだとすると残り $2$ 点は $( {\rm B}, {\rm F})$ か $({\rm E}, {\rm C})$ のいずれか。よって, このパターンの総数は

$$
\begin{align}
&{} \hspace{5mm} (V \, {\rm の選び方}) \times (V \, {\rm 上の} \, 2 \, {\rm 点の選び方}) \times (W \, {\rm の選び方}) \\
&{} \hspace{10mm} \times (\{ {\rm J}, \, {\rm K}, \, {\rm L} \} \, {\rm からの選び方}) \\
&{} \hspace{10mm} \times (\{ {\rm A}, \, {\rm B}, \, {\rm C}, \, {\rm D}, \, {\rm E}, \, {\rm F} \} \, {\rm からの選び方}) \\
&= 4 \times {}_{4} {{\rm C}}_{2} \times 2 \times 3 \times 2 = 288
\end{align}
$$

より $288$ 通りである。

(b) $V$ と $W$ の交点が選ばれない場合

$W$ は上図の位置であったとする。このとき, $\{ {\rm A}, \, {\rm B}, \, {\rm C} \}$ から $2$ つ選び, $\{ {\rm D}, \, {\rm E}, \, {\rm F}, \, {\rm G}, \, {\rm H}, \, {\rm I} \}$ から $1$ つ

選ぶこととなる。 $\{ {\rm A}, \, {\rm B}, \, {\rm C} \}$ からの選び方は $3$ 通りであり, たとえば $({\rm A}, \, {\rm B})$ を選んだとすると残り $1$ 点は ${\rm F}$ と定まる。したがって, このパターンの総数は

$$
\begin{align}
&{} \hspace{5mm} (V \, {\rm の選び方}) \times (V \, {\rm 上の} \, 2 \, {\rm 点の選び方}) \times (W \, {\rm の選び方}) \\
&{} \hspace{10mm} \times (\{ {\rm A}, \, {\rm B}, \, {\rm C} \} \, {\rm からの選び方}) \\
&{} \hspace{10mm} \times (\{ {\rm D}, \, {\rm E}, \, {\rm F}, \, {\rm G}, \, {\rm H}, \, {\rm I} \} \, {\rm からの選び方}) \\
&= 4 \times {}_{4} {{\rm C}}_{2} \times 2 \times 3 \times 1 = 144
\end{align}
$$

より $144$ 通り。

以上より, 条件をみたす点の選び方の総数は $288 + 144 = \underline{432}$ 通りである。

数え上げの問題では "漏れなく・重複なく" というのがカギです。
この一見当然であることをいかに徹底できるかが, 数え上げの問題で正解できるか否かを左右しているといっても過言ではありません。

場合分けの際,