【A級紙】 #07 等角螺旋の弧長 ～極方程式と図形的考察～

前回は直交座標での弧長の公式を紹介しましたが，今回は極座標表示されたグラフの弧長について考えます。
公式は次の通りです。

極方程式 $r = r(\theta) \quad (\alpha \leq \theta \leq \beta)$ で与えられる曲線の長さ $s$ は

$\hspace{5mm} s = \displaystyle\int_{\alpha}^{\beta} \sqrt{r^2 + \left( \displaystyle\frac{dr}{d\theta} \right)^2} \, d\theta$

と表せる。

極方程式で表される曲線の長さの公式

なぜこのように求められるのか，前回同様に考えてみましょう。
※厳密な証明ではなく，上のような形になる理由の考察です。

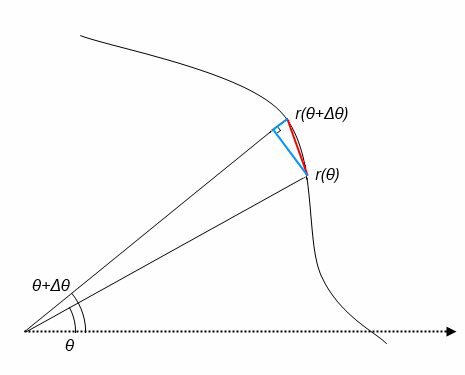
曲線上の 2 点を結ぶ，図の赤線部の長さ $\Delta s$ は，三平方の定理より

$$
\begin{align}
\Delta s &= \sqrt{\left( r \sin \Delta \theta \right)^2 + \left( r ( \theta + \Delta \theta ) - r ( \theta ) \right)^2}
\end{align}
$$

と求めることができます。$\Delta \theta$ が十分小さい量であるとき $\sin \Delta \theta \simeq \Delta \theta$ が成り立つことも踏まえると，

$$
\begin{align}
\Delta s &\simeq \sqrt{\left( r \Delta \theta \right)^2 + \left( r ( \theta + \Delta \theta ) - r ( \theta ) \right)^2} \\
&= \sqrt{r^2 + \left( \displaystyle\frac{r ( \theta + \Delta \theta ) - r ( \theta )}{\Delta \theta} \right)^2} \, \Delta \theta \\
&= \sqrt{r^2 + \left( \displaystyle\frac{\Delta r}{\Delta \theta} \right)^2} \, \Delta \theta
\end{align}
$$

が成り立ちます。ここで $\Delta \theta \to 0$ の極限をとれば赤線の長さは微小となり，ほぼ 2 点間を結ぶ曲線の長さに等しいと見なせるようになるから，$\theta = \alpha$ から $\theta = \beta$ まで $\theta$ を連続的に変化させて $\Delta s$ を足し合わせたものが $s$ であると考えれば，さきの公式が得られます。

こうした公式のお陰で様々なグラフの長さを求めることができるようになるわけですが，逆にこれが無ければ曲線の長さは求められないのかというと，もちろんそういう訳ではありません。
特にグラフが何か特徴的な図形的性質をもっているとき，その性質を上手く利用することで公式を用いずとも曲線の長さを求められる場合があります。

このことを体現した問題が東大理系数学 2007 年第 2 問。
これもまた表面的には計算問題なのですが，中身をよく見てみれば実にうまいこと曲線の長さを求めています。
計算練習のつもりで次の問題を解き，これを実感してみることにしましょう。

---

問 題

$n$ を $2$ 以上の整数とする。平面上に $n+2$ 個の点 ${\rm O}, \, {\rm P}_{0}, \, {\rm P}_{1}, \, \cdots, \, {\rm P}_{n}$ があり，次の 2 つの条件をみたしている。

① $\angle{{\rm P}_{k-1} {\rm O} {\rm P}_{k}} = \displaystyle\frac{\pi}{n} \, (1 \leqq k \leqq n),$
　$\, \angle{{\rm O} {\rm P}_{k-1} {\rm P}_{k}} = \angle{{\rm OP_{0} P_{1}}} \, (2 \leqq k \leqq n)$

② 線分 ${\rm OP_{0}}$ の長さは $1$,
　 線分 ${\rm OP_{1}}$ の長さは $1 + \displaystyle\frac{1}{n}$ である。

線分 ${\rm P}_{k-1} {\rm P}_{k}$ の長さを $a_{k}$ とし，$s_{n} = \displaystyle\sum_{k = 1}^{n} a_{k}$ とおくとき，$\displaystyle\lim_{n \to \infty} s_{n}$ を求めよ。

2007年度 東京大学 理系数学 第2問 より。

解 説

$\triangle{}{\rm O P_{0} P_{1}} \sim \triangle{}{\rm OP_{1}P_{2}} \sim \cdots$（$\sim$ は相似を意味する）となるため，相似比を考えることで

$a_{k} = {\rm P_{0}P_{1}} \times \left( 1 + \displaystyle\frac{1}{n} \right)^{k-1}$

を得る。また余弦定理より

${\rm P_{0}P_{1}} = \sqrt{1 + \left( 1 + \displaystyle\frac{1}{n} \right)^2 - 2 \left( 1 + \displaystyle\frac{1}{n} \right) \cos \displaystyle\frac{\pi}{n}}$

であるから

$$
\begin{align}
&\displaystyle\lim_{n \to \infty} s_{n} \\
&= \displaystyle\lim_{n \to \infty} {\rm P_{0}P_{1}} \cdot \displaystyle\sum_{k = 1}^{n} \left( 1 + \displaystyle\frac{1}{n} \right)^{k-1} \\
&= \displaystyle\lim_{n \to \infty} \left\{ \left( 1 + \displaystyle\frac{1}{n} \right)^n - 1 \right\} \\
&{} \hspace{10mm} \cdot n \sqrt{1 + \left( 1 + \displaystyle\frac{1}{n} \right)^2 - 2 \left( 1 + \displaystyle\frac{1}{n} \right) \cos \displaystyle\frac{\pi}{n}} \\
&= \displaystyle\lim_{n \to \infty} \left\{ \left( 1 + \displaystyle\frac{1}{n} \right)^n - 1 \right\} \\
&{} \hspace{10mm} \cdot \sqrt{n^2 + \left( n + 1 \right)^2 - 2 \left( n^2 + n \right) \cos \displaystyle\frac{\pi}{n}}
\end{align}
$$

という式で求めることができる。ここで

$\displaystyle\lim_{n \to \infty} \left\{ \left( 1 + \displaystyle\frac{1}{n} \right)^n - 1 \right\} = e - 1$

であり，

$$
\begin{align}
&{} n^2 + \left( n + 1 \right)^2 - 2 \left( n^2 + n \right) \cos \displaystyle\frac{\pi}{n} \\
&= 2 n^2 \left( 1 - \cos \displaystyle\frac{\pi}{n} \right) + 2n \left( 1 - \cos \displaystyle\frac{\pi}{n} \right) + 1 \\
&= 4n^2 \sin^2 \displaystyle\frac{\pi}{2n} + 4n \sin^2 \displaystyle\frac{\pi}{2n} + 1 \\
&= \pi^2 \cdot \displaystyle\frac{\sin^2 \displaystyle\frac{\pi}{2n}}{\left( \displaystyle\frac{\pi}{2n} \right)^2} + \displaystyle\frac{\pi^2}{n} \cdot \displaystyle\frac{\sin^2 \displaystyle\frac{\pi}{2n}}{ \left( \displaystyle\frac{\pi}{n} \right)^2} + 1 \\
&\to \pi^2 + 1 \quad (n \to \infty)
\end{align}
$$

となるから，

$\displaystyle\lim_{n \to \infty} s_{n} = \underline{(e - 1) \sqrt{\pi^2 + 1}}$

となる。

---

このように，曲線をたくさんの線分の集まりで近似し，その分割を限りなく細かく分割することにより，曲線の長さを求めることができます。

上の東大の問題では単に線分の長さの極限を問われているだけで，それが曲線長であることや，それ以外の発展事項については触れられていません。（入試問題ですから当然ですね。）

そこで，上の問題に発展事項をたくさん載せて，改題してみました。

興味のある人はこちらの問題にもチャレンジしてみましょう！

---

追 加 問 題

追加問題（注意：それっぽい見た目にしていますが，(2) 以降は東大の入試問題ではありません。

追 加 問 題 の 略 解

(1) 先述の通り。

(2)

面積比を考えることで $b_{k} = \triangle{{\rm OP_{0}P_{1}}} \cdot \left( 1 + \displaystyle\frac{1}{n} \right)^{2(k-1)}$ を得る。$\triangle{{\rm OP_{0}P_{1}}} = \displaystyle\frac{1}{2} \cdot 1 \cdot \left( 1 + \displaystyle\frac{1}{n} \right) \cdot \sin \displaystyle\frac{\pi}{n}$ であるから

$$
\begin{align}
&{} \displaystyle\lim_{n \to \infty} t_{n} \\
&= \displaystyle\lim_{n \to \infty} \triangle{{\rm OP_{0}P_{1}}} \cdot \displaystyle\sum_{k = 1}^{n} \left( 1 + \displaystyle\frac{1}{n} \right)^{2(k-1)} \\
&= \cdots ({\rm やや面倒ですが自分で計算してみましょう！}) \\
&= \displaystyle\frac{1}{4} \pi (e^2 - 1) \quad \cdots 答
\end{align}
$$

(3)

点 ${\rm P}_{k}$ の極からの距離は ${\rm OP}_{k} = \left( 1 + \displaystyle\frac{1}{n} \right)^{k}$，偏角は $\theta = \displaystyle\frac{k\pi}{n}$（ただし，$0 \leq k \leq n$ より $0 \leq \theta \leq \pi$）で表せる。よって $k$ を消去し，$r$ と $\theta$ の関係を表せば

$r = \left\{ \left( 1 + \displaystyle\frac{1}{n} \right)^n \right\}^{\frac{\theta}{\pi}} \to e^{\frac{\theta}{\pi}} \quad (0 \leq \theta \leq \pi) \quad \cdots 答$

(4), (5)

与えられた積分に (3) の結果式 $r = e^{\frac{\theta}{\pi}}$ を代入して計算すれば，(1), (2) と合わせて問題文の式が成り立つことが示される。

---

おまけ： $n$ の値と折れ線の様子

せっかくの視覚化の機会なので，ちょっと作図してみました。

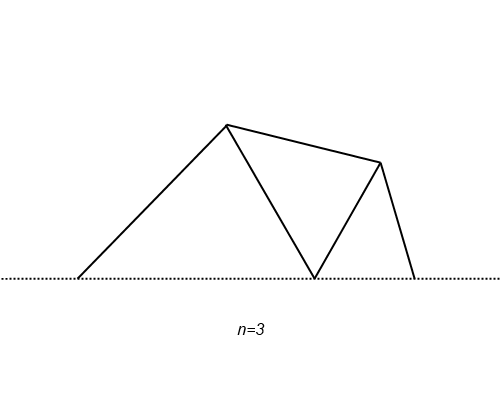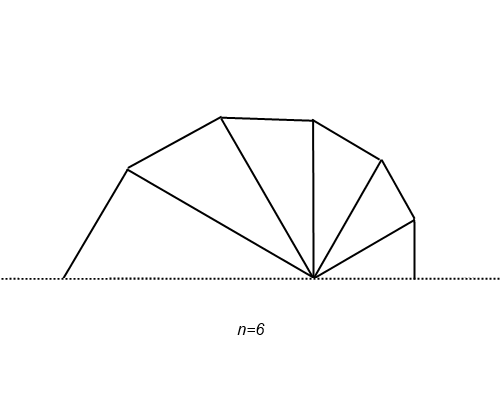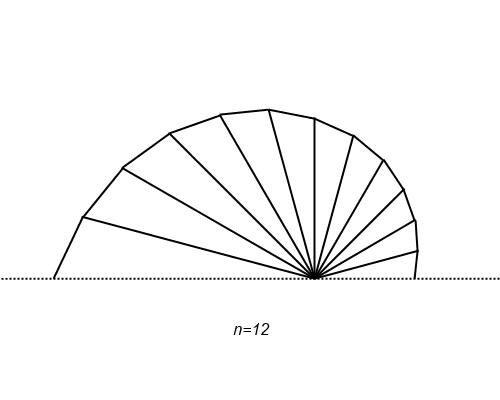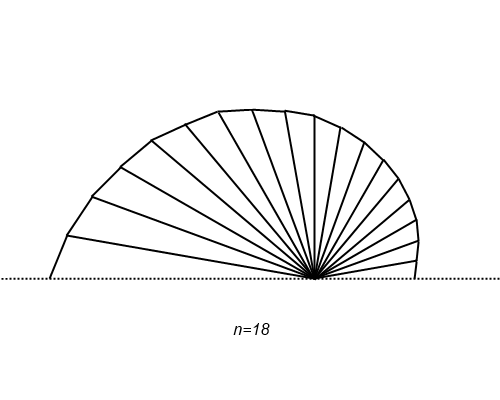
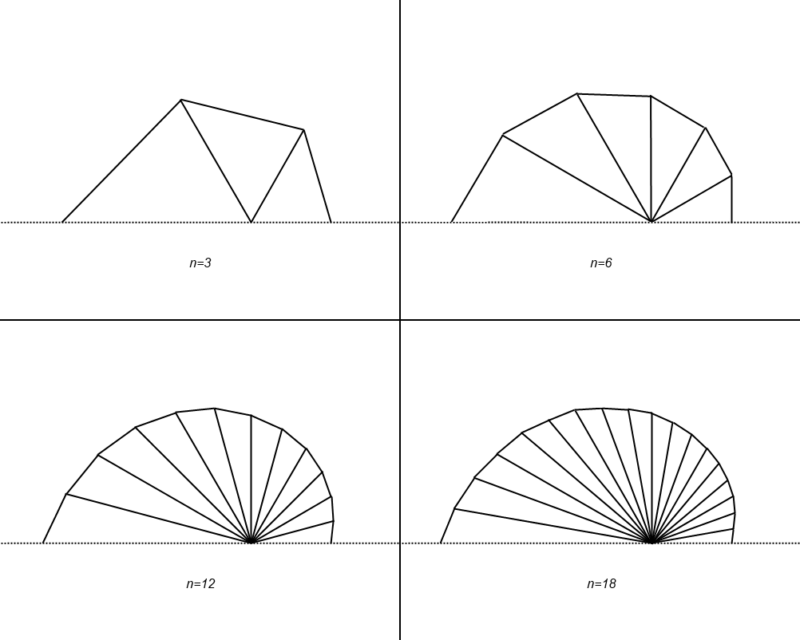
段々なめらかになって，ある曲線に収束する様子が確かめられますね。もちろん，その曲線は $r = e^{\frac{\theta}{\pi}}$
点 ${\rm P}_{n}$ の位置を見ることで，自然対数の底 $e$ の定義式にある $\left( 1 + \displaystyle\frac{1}{n} \right)^n$ は，$n$ について単調に増加するということにも気がつきます。