【東大数学分野別解説】#10 実は最近多い "平面図形"

2022.02.08

この連載では，東大数学の過去問の中から学びの多そうなものを分野別に解説していきます。単に正解を述べるだけでなく，問題を解く際のアプローチや補足事項も添えるので，初見の問題への対応力も磨けることでしょう。

難関大の入試というと，微分・積分などの解析計算や整数問題，確率の問題などをイメージする人が多いかもしれません。
しかし，近年の東大入試では地味ながらも "平面図形" に関連する問題がよく出題されています。
そこで今回は，近年の東大入試で出題されている図形問題をご紹介します。

問題 1

平面上の点 ${\rm P, \, Q, \, R}$ が同一直線上にないとき，それらを 3 頂点とする三角形の面積を $\triangle{{\rm PQR}}$ で表す。また，${\rm P, \, Q, \, R}$ が同一直線上にあるときは $\triangle{{\rm PQR}} = 0$ とする。
${\rm A, \, B, \, C}$ を平面上の 3 点とし，$\triangle{{\rm ABC}} = 1$ とする。この平面上の点 ${\rm X}$ が
$$
\begin{align}
2 \leqq \triangle{{\rm ABX}} + \triangle{{\rm BCX}} + \triangle{{\rm CAX}} \leqq 3
\end{align}
$$
を満たしながら動くとき，${\rm X}$ の動きうる範囲の面積を求めよ。
2020年度東京大学理系数学第2問

問題 1 の解答

この三角形をなす $3$ 辺を直線として延長すると，平面は次のような $7$ つの領域に分割される。

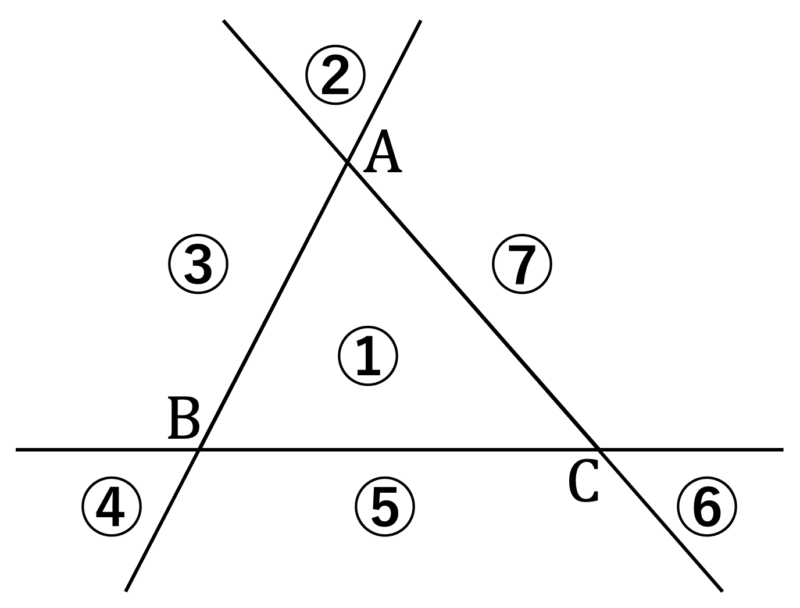
以下，点 ${\rm X}$ がこれら $7$ 領域のうちどこにあるかで分類する。
(②・④・⑥ と ③・⑤・⑦ は対等であり，同じ議論が適用できることに注意。)

(i) 点 ${\rm X}$ が領域 ① にあるとき

このとき $\triangle{{\rm ABX}} + \triangle{{\rm BCX}} + \triangle{{\rm CAX}} = \triangle{{\rm ABC}} = 1$ であり，問題文の不等式は成り立たない。

(ii) 点 ${\rm X}$ が領域 ②・④・⑥ にあるとき

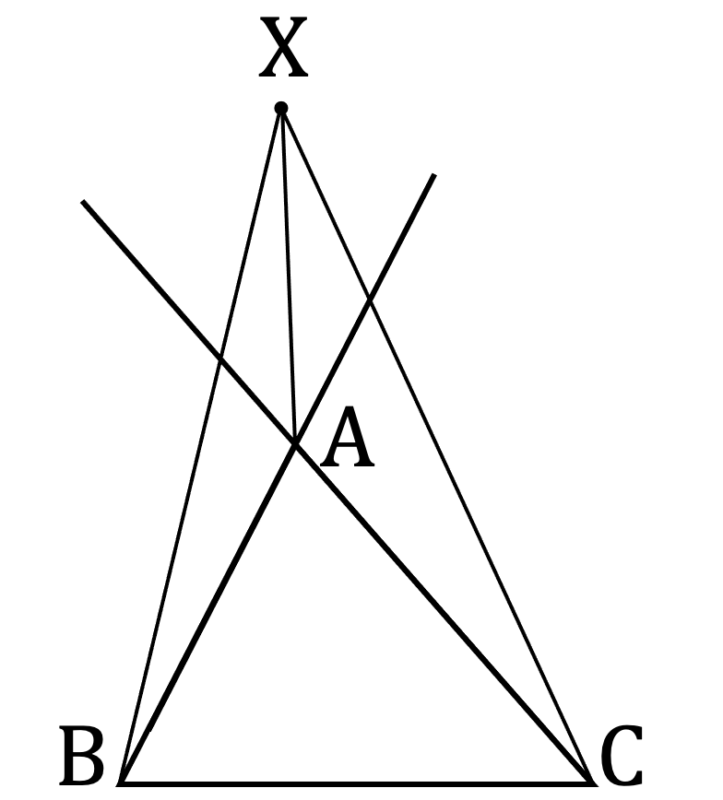
このとき，直線 ${\rm BC}$ を基準としたときに点 ${\rm X}$ の高さを点 ${\rm A}$ の $h_{1}$ 倍とすると

$$
\begin{align}
&{} \hspace{10mm} \triangle{{\rm ABX}} + \triangle{{\rm BCX}} + \triangle{{\rm CAX}} \\
&= 2 \triangle{{\rm XBC}} - \triangle{{\rm ABC}} \\
&= 2 h_{1} - 1
\end{align}
$$

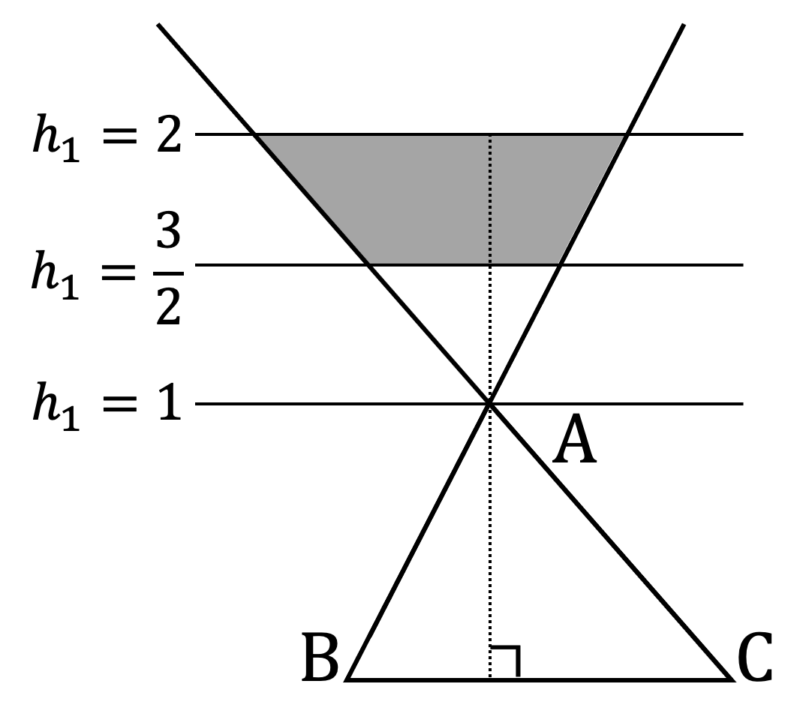
となる。よって，問題文の不等式が成り立つための必要十分条件は $2 \leqq 2 h_{1} - 1 \leqq 3$ つまり $\displaystyle\frac{3}{2} \leqq h_{1} \leqq 2$ であり，これをみたす領域は次のようになる。

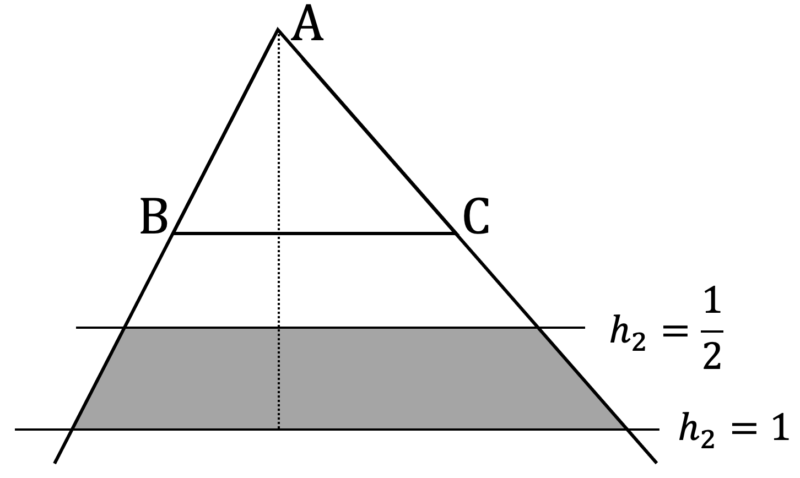
(iii) 点 ${\rm X}$ が領域 ②・④・⑥ にあるとき

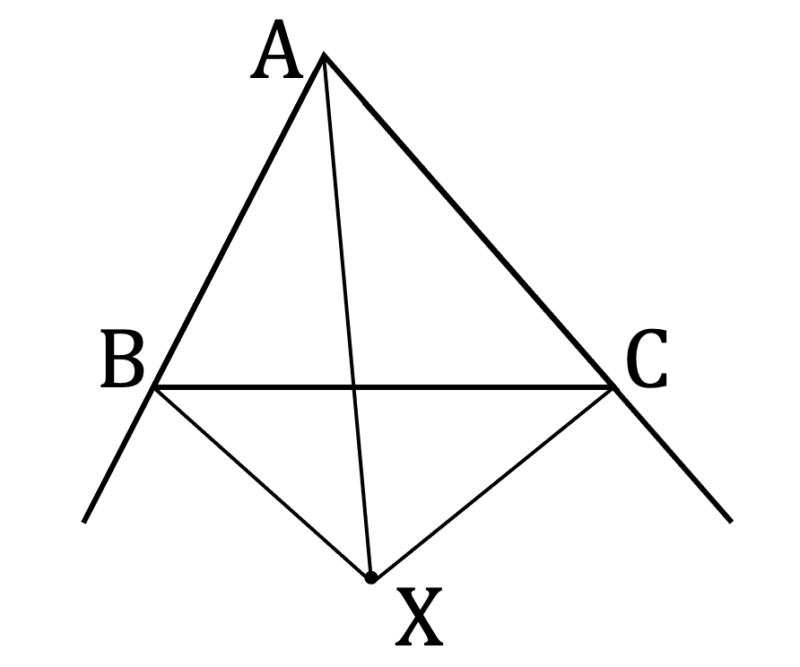
このとき，直線 ${\rm BC}$ を基準としたときに点 ${\rm X}$ の高さを点 ${\rm A}$ の $h_{2}$ 倍とすると

$$
\begin{align}
&{} \hspace{10mm} \triangle{{\rm ABX}} + \triangle{{\rm BCX}} + \triangle{{\rm CAX}} \\
&= \triangle{{\rm ABC}} + 2 \triangle{{\rm XBC}} \\
&= 1 + 2 h_{2}
\end{align}
$$

となる。よって，問題文の不等式が成り立つための必要十分条件は $2 \leqq 1 + 2 h_{2} \leqq 3$ つまり $\displaystyle\frac{1}{2} \leqq h_{1} \leqq 1$ であり，これをみたす領域は次のようになる。

以上より，問題文の不等式をみたす点 ${\rm X}$ がうごく領域は次のようになる。

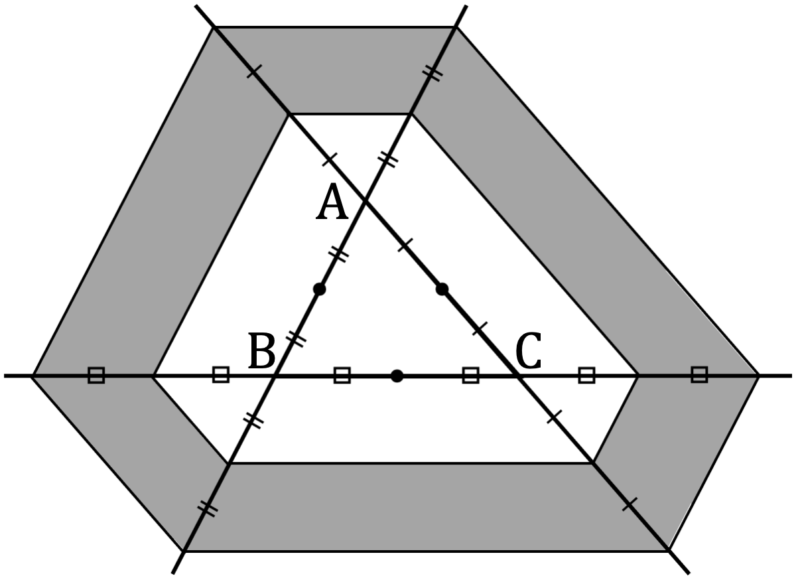
このうち，②・④・⑥ にある部分の面積はそれぞれ $\displaystyle\frac{3}{4}$ であり，③・⑤・⑦ にある部分の面積はそれぞれ $\displaystyle\frac{7}{4}$ であるため，求める面積の合計は

$$
\begin{align}
3 \times \frac{3}{4} + 3 \times \frac{7}{4} = \underline{\frac{15}{2}}
\end{align}
$$

となる。

問題 1 のポイント・補足

このように，具体的な数量が与えられていない図形問題では，ベクトルや座標を設定するよりも "図形のまま眺める" 方が解きやすいです。
普段の勉強で図形問題を計算でゴリ押してばかりいるとこうした問題で苦労してしまうことでしょう。ときにはこうして，図形を図形として扱うのも大切です。

問題 2

一辺の長さが $1$ の正方形 ${\rm ABCD}$ を考える。$3$ 点 ${\rm P, \, Q, \, R}$ はそれぞれ辺 ${\rm AB, \, AD, \, CD}$ 上にあり，$3$ 点 ${\rm A, \, P, \, Q}$ および $3$ 点 ${\rm P, \, Q, \, R}$ はどちらも面積が $\displaystyle\frac{1}{3}$ の三角形の $3$ 頂点であるとする。
$\displaystyle\frac{{\rm DR}}{{\rm AQ}}$ の最大値，最小値を求めよ。
2019年度東大理系数学第2問 (文系数学もほぼ同じ問題です。)

問題 2 の解答

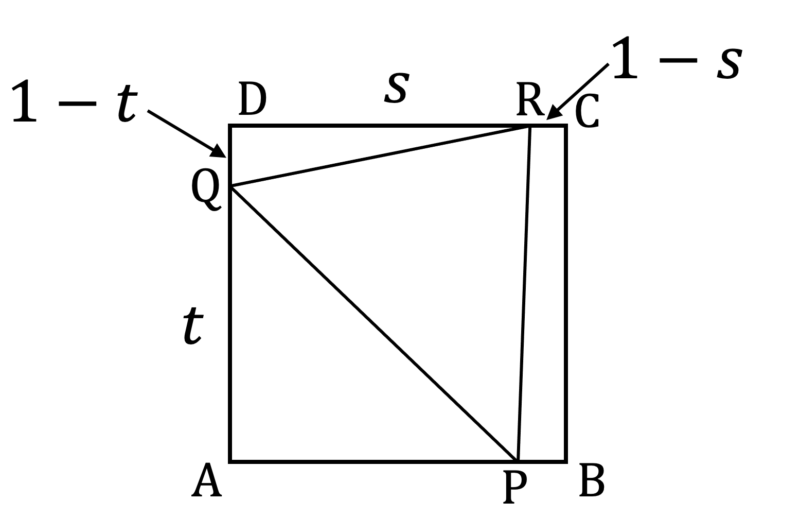
${\rm AQ} = t \, (0 < t \leqq 1)$ とする。

$\triangle{{\rm APQ}} = \displaystyle\frac{1}{3}$ より ${\rm AP} = \displaystyle\frac{2}{3t}$ であり，点 ${\rm P}$ が辺 ${\rm AB}$ 上にあることから $0 < \displaystyle\frac{2}{3t} \leqq 1$ が必要となる。つまり，$\triangle{{\rm APQ}} = \displaystyle\frac{1}{3}$ であるとき $t$ は $\displaystyle\frac{2}{3} \leqq t \leqq 1$ の範囲を動く。

次に ${\rm DR} = s \, (0 \leqq s \leqq 1)$ とし，これを $t$ で表す。$\triangle{{\rm DQR}}$ の面積は $\displaystyle\frac{1}{2} (1-t)s$ であり，四角形 ${\rm PBCR}$ の面積は $\left\{ \left( 1 - \displaystyle\frac{2}{3t} \right) + (1-s) \right\} \cdot 1 \cdot \displaystyle\frac{1}{2} = 1 - \displaystyle\frac{1}{3t} - \displaystyle\frac{1}{2} s$ となるが，これらの合計は $\displaystyle\frac{1}{3}$ であるため

$$
\begin{align}
\frac{1}{2} (1-t)s + 1 - \frac{1}{3t} - \frac{1}{2} s &= \frac{1}{3} \\
\therefore s = \frac{2}{3t} \left( 2 - \frac{1}{t} \right) &{}
\end{align}
$$

となる。

ここで新たに $u = \displaystyle\frac{1}{t}$ とする。$u$ は $1 \leqq u \leqq \displaystyle\frac{3}{2}$ の範囲を動くが，この範囲における $s = \displaystyle\frac{2}{3} u (2 - u)$ の値域は $\displaystyle\frac{1}{2} \leqq s \leqq \displaystyle\frac{2}{3}$ となる。よって，点 ${\rm P}$ が辺 ${\rm AP}$ 上に，点 ${\rm Q}$ が辺 ${\rm AD}$ 上にあるならば，$\triangle{{\rm PQR}} = \displaystyle\frac{1}{3}$ となる点 ${\rm R}$ は辺 ${{\rm DC}}$ 上に存在する。よって，$1 \leqq u \leqq \displaystyle\frac{3}{2}$ における

$$
\begin{align}
\frac{{\rm DR}}{{\rm AQ}} = \frac{2}{3 t^2} \left( 2 - \frac{1}{t} \right) = \frac{2}{3} u^2 (2 - u)
\end{align}
$$

の最大値・最小値を求めればよい。$f(u) := \displaystyle\frac{2}{3} u^2 (2-u)$ とすると，$f'(u) = \displaystyle\frac{2}{3} \left( 4u - 3u^2 \right) = -2 u \left( u - \displaystyle\frac{4}{3} \right)$ となるため，関数 $f(u)$ は $1 \leqq u \leqq \displaystyle\frac{4}{3}$ で単調に増加し，$\displaystyle\frac{4}{3} \leqq u \leqq \displaystyle\frac{3}{2}$ で単調に減少する。よってこの区間における $f(u)$ の最大値は $f \left( \displaystyle\frac{4}{3} \right) = \displaystyle\frac{64}{81}$ であり，最小値は $\min \left\{ f(1), \, f \left( \displaystyle\frac{3}{2} \right) \right\} = f (1) = \displaystyle\frac{2}{3}$ である。

$$
\begin{align}
\displaystyle\frac{{\rm DR}}{{\rm AQ}} {\rm の最大値は} \frac{64}{81}, \quad {\rm 最小値は} \frac{2}{3} \cdots 答
\end{align}
$$

問題 2 のポイント・補足

$\displaystyle\frac{{\rm DR}}{{\rm AQ}}$ を ${\rm AQ}$ の関数として表すと分数関数になってしまいますが，${\rm AQ}$ の逆数で表すとシンプルな多項式になり，最大値・最小値を求めやすくなります。分数関数のままでも，理系数学の範囲であれば増減の計算ができますが，解説のようにシンプルな関数に変形して取り扱うことで，計算ミスのリスクを減らすことができます。