東大志望の受験生のためのサイト

第14回　出典：東京大学前期　2007年　理系数学　第2問

　皆さん、こんにちは。殆どの理系の東大受験生は、入試当日を迎えるまでに「今年の物理第3問は去年波だったから熱になるんじゃないか」とかいった話を友達とするんじゃないかと思うんですが、いかがでしょう。当然のことですが、どっちかにヤマを張るなんてことのないように。波の次は熱なんてルール、誰も決めてないんですからね。A級紙だって、数学の次が化学だなんて一言も言ってません。そういう訳で（？）、今回は前回に続き数学でお送りします。笑

　前回は直交座標での弧長の公式を紹介しましたが、今回は極座標表示されたグラフの弧長について考えます。公式は次の通り。

　極方程式

　　　

で与えられる曲線の長さ s は、

と表せる.

　どうしてこうなるのかについては、前回と同様に考えてみましょう。

　曲線上の2点を結ぶ、図の赤線部の長さ Δs は、三平方の定理から

　　

　ここで Δθ → 0 の極限を取れば赤線の長さは微小となり、ほぼ2点間を結ぶ曲線の長さに等しいと見なせるようになるから、θ=α から θ=β まで θ を連続的に変化させて Δs を足し合わせたものが s であると考えれば、上の公式を得る.
（※まあ、前回の公式で θ をパラメータとし x=r cosθ , y=r sinθ として計算しても同じなんですけどね.）

　こういった公式のお陰で様々なグラフの長さを求めることができるようになる訳ですが、逆にこれが無ければ曲線の長さは求められないのかというと、勿論そういう訳ではありません。特にグラフが何か特徴的な図形的性質を持っているとき、その性質を上手く利用することで公式を用いずとも曲線の長さを求められる場合があります。このことを体現した問題が東大理系数学2007年第2問。これもまた表面的には計算問題なのですが、中身をよく見てみれば実に上手いこと曲線の長さを求めています。計算練習のつもりで次の問題を解き、これを実感してみてください。

⇒問題（PDF）

⇒略解


　せっかくの機会なので、上の問題では極座標における動径の掃過面積の公式まで確かめてみました。

　極方程式

　　　

において動径が掃過する部分の面積 S は、

と表せる.

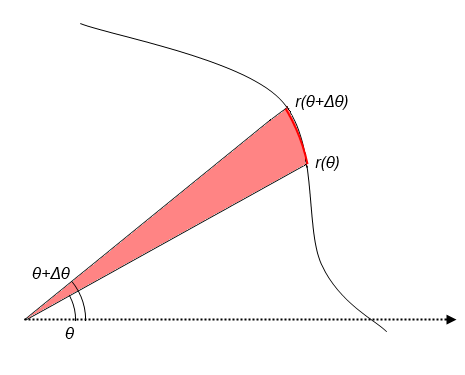
　図で色を付けた半径 r(θ) の扇形の面積 ΔS は、

　ここで Δθ → 0 の極限を取れば赤線の長さは微小となり、ほぼ動径が曲線上の2点間を動くときに掃過する領域の面積に等しいと見なせるようになるから、θ=α から θ=β までθを連続的に変化させて ΔS を足し合わせたものが S であると考えれば、上の公式を得る.
（※もう少し厳密には、大きい扇形と小さい扇形で ΔS を評価してハサミウチの原理を使えばok.）

　計算方法も一通り確認できたところで、今回の図形を見てみましょう。極方程式で

と表される曲線の一部が、n→∞ で現れる曲線 C だというのは問題で見た通り。このように の形で表される曲線を“等角螺旋”と言って、これまた大学入試で別段重要な曲線という訳じゃないんですが、概形はこんな感じ。

▲等角螺旋

※ a=1.0、b=1/π として作図

　どうでしょう、前回の双曲螺旋よりも、皆さんの思い描く“螺旋”のイメージに近くありませんか？　実は、多くの貝殻に現れる模様がこの等角螺旋であることが知られています。

　　　

▲見比べてみよう

　貝殻の他にも、ツメやツノ、キバなど、放っておくとどんどん伸びていくような動物の硬い部位に、この等角螺旋はしょっちゅう現れます。これがなぜなのか、ざっくり考えてみましょう。

　今回の問題で、相似な三角形が一辺を共有して連なっていくその極限として等角螺旋が現れることを確認しました。三角形にできることは、一般の多角形――もっと言えば一般の図形でもできるはずです（等角螺旋を作っている三角形を、螺旋に関わる部分だけ残るように分割すると考えれば良い）。すなわち、相似な図形がその一部で接しながら連続していく過程に等角螺旋が現れるわけです。ここで、例えばツノがどのように伸びていくのか考えてみると、勿論根元から少しずつ生えてくるのでしょうが、その様子は「連続的」で、生えてきたばかりの微小部分に着目すればその形状はおそらくいつも同じはず、すなわち「相似」なはずです。この微小部分が一部を共有しながら――「接しながら」、連なって成長していくわけで、この流れはツノ以外でも多分同じ。どうでしょう、等角螺旋が現れるのに、動物の成長には十分な条件が揃っていると言えるのではないでしょうか。


　等角螺旋には、

・接線がその接点で動径と為す角度は一定である（だから“等角”螺旋と呼ぶ）
・原点を中心として回転移動する操作は、原点を基準として拡大する操作と等価である
・原点付近で無限回渦巻くが、原点までの弧長の極限は有限の値を持つ

など、興味深い性質がまだまだ秘められていますが（これらについては難しくないので是非考えてみてください）、今回はその中で“動物の体に現れる”というただそれだけの、しかし視覚的にとてもvividなことを純粋に楽しんでみました。“貝の渦巻き”なんてどこから手をつけたらいいかわからないようなものに対しても、図形的に何らかの説明が出来てしまうとは驚きですね。

　また、今回の記事の前半では高校程度を超える積分公式の代用として、図形的な考え方が生きることも見てもらったと思います。定性的にも定量的にも、図形の観点は大活躍ですね。図形的要素が絡む問題に対し、必要に応じて必要な図形的性質を持ってくることは多くの場合効果的ですし、これは入試問題にも言えること。とりわけ東京大学の数学には、2004年文理共通第1問や2010年理系第4問など“計算だけでゴリ押すには大変だけれど図形的な性質を上手く使えればスマートに解ける良問”がしばしば登場していて、なおかつその問題が当該のセットで明暗を分ける構成になっていることも少なくありません。

　大事なのは、いつも図形で考えろというのではなく、然るべき時に然るべき図形的観点に立てるようになっておけということです。そのセンスを磨くために、普段から図形というものに慣れ親しんでおきたいところですね。題材は身のまわりにもまだまだ結構ありますから、それこそ勉強帰り、夜道に自転車を走らせるときにでも探してみてはいかがでしょう。灯台下暗しかもしれませんよ。それではまた次回。

2014/02/07 石橋雄毅