【東大数学分野別解説】#13 いつどこで出るかわからない "二次曲線"

東大理系数学の過去問を見てみると，二次曲線がメインテーマとなっている出題が極端に少ないことがわかります。(数学III の中では目立って少ないです。)
しかし，軌跡を求める問題で突然最終結果に二次曲線が現れる，という問題もあります。
そこで今回は，

• 二次曲線そのものの性質を問う問題
• 二次曲線が題材となっているが，そこまでメインではない問題
• 軌跡を求めた結果が二次曲線になる問題

をピックアップし，東大理系数学においてさまざまな形で二次曲線が登場することを知っていただこうと思います。

---

問 題 1

$\mathrm{O}$ を原点とする座標平面上の曲線
$$\begin{array}{r}C:y=\frac{1}{2}x+\sqrt{\frac{1}{4}{x}^2+2}\end{array}$$

と，その上の相異なる $2$ 点 ${\mathrm{P}}_1(x_1,y_1),{\mathrm{P}}_2(x_2,y_2)$ を考える。

(1) ${\mathrm{P}}_i(i=1,2)$ を通る $x$ 軸に平行な直線と，直線 $y=x$ との交点を，それぞれ ${\mathrm{H}}_i(i=1,2)$ とする。このとき $\mathrm{△}\mathrm{O}{\mathrm{P}}_1{\mathrm{H}}_1$ と $\mathrm{△}\mathrm{O}{\mathrm{P}}_2{\mathrm{H}}_2$ の面積は等しいことを示せ。

(2) $x_1<x_2$ とする。このとき $C$ の $x_1\leqq x\leqq x_2$ の範囲にある部分と，線分 ${\mathrm{P}}_1\mathrm{O},{\mathrm{P}}_2\mathrm{O}$ とで囲まれる図形の面積を，$y_1,y_2$ を用いて表せ。

2010年 東大 理系数学 第4問

---

問 題 1 の 解 答

(1)

任意の実数 $x$ に対し ${\displaystyle \frac{1}{2}}<\sqrt{{\displaystyle \frac{1}{4}}{x}^2+2}$ となることに注意する。点 ${\mathrm{H}}_{\mathrm{i}}$ の座標は $(y_i,y_i)$ であるため，$\mathrm{△}\mathrm{O}{\mathrm{P}}_{\mathrm{i}}{\mathrm{H}}_{\mathrm{i}}$ の面積は

$$\begin{array}{r}\frac{1}{2}\cdot (y_i-x_i)\cdot y_i=\frac{1}{2}(y_i^2-x_i{y}_i)\end{array}$$

である。ここで，${\mathrm{P}}_i$ は曲線 $C$ 上にあるため，

$$\begin{array}{rl}{y}_i& =\frac{1}{2}{x}_i+\sqrt{\frac{1}{4}{x}_i+2}\\ {(y_i-\frac{1}{2}{x}_i)}^2& =\frac{1}{4}{x}_i^2+2\\ y_i^2-x_i{y}_i& =2\end{array}$$

が成り立つ。ゆえに $\mathrm{△}\mathrm{O}{\mathrm{P}}_{\mathrm{i}}{\mathrm{H}}_{\mathrm{i}}$ の面積は ${\displaystyle \frac{1}{2}}\cdot 2=1$ で一定である。■

(2)

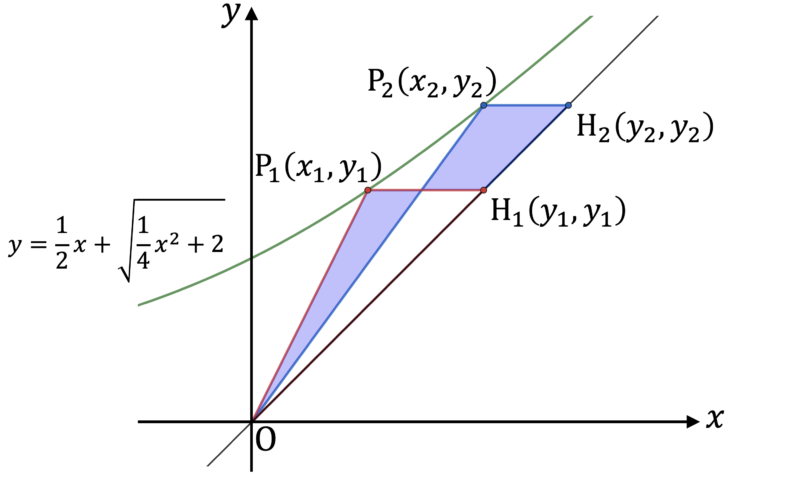
(1) の結果より，図の色をつけた部分の面積は等しくなる。よって，求める面積は曲線 $C$ と直線 $y=x$，そして線分 ${\mathrm{P}}_1{\mathrm{H}}_1,{\mathrm{P}}_2{\mathrm{H}}_2$ で囲まれる領域の面積と等しい。曲線 $C$ の方程式が $x=y-{\displaystyle \frac{2}{y}}(y>0)$ であることも踏まえると，この面積は

$$\begin{array}{r}{\int }_{y_1}^{y_2}\{y-(y-\frac{2}{y})\}dy={[2\log y]}_{y_1}^{y_2}=2\log \frac{y_2}{y_1}\end{array}$$

と計算できる。

---

問 題 1 の ポ イ ン ト ・ 補 足

二次曲線の性質そのものに関する出題でした。先述の通り，この類の出題は結構レアです。
一見二次曲線に見えませんが，これは傾いた双曲線の形をしています。
${\displaystyle \frac{x^2}{a^2}}-{\displaystyle \frac{y^2}{b^2}}=\pm 1$ の形の双曲線においても同様の性質が成り立つため，興味のある人はぜひ調べてみてください。

---

問 題 2

$\alpha ,\beta$ を正の数とし，$xy$ 平面において，だ円

$$\begin{array}{r}C:\frac{x^2}{\alpha }+\frac{{(y-\sqrt{\beta })}^2}{\beta }=1\end{array}$$

と領域 $D=\{(x,y)|x^2+y^2\leqq 1\}$ を考える。

(1) $C$ が $D$ に含まれるような点 $(\alpha ,\beta )$ の範囲を求め，$\alpha \beta$ 平面上に図示せよ。

(2) 点 $(\alpha ,\beta )$ が (1) で求めた範囲を動くとき，だ円 $C$ の面積の最大値を求めよ。

1996年 東大 理系数学 第6問

---

問 題 2 の 解 答

(1)

楕円 $C$ の中心は $(0,\sqrt{\beta })$ であり，$x$ 軸方向の半径は $\sqrt{\alpha }$，$y$ 軸方向の半径は $\sqrt{\beta }$ である。

楕円上の任意の点は，ある $0\leqq \theta <2\pi$ なる実数 $\theta$ を用いて $(\sqrt{\alpha }\cos \theta ,\beta (1+\sin \theta ))$ と表せる。この点の原点からの距離を $l(\theta )$ とすると

$$\begin{array}{rl}l(\theta {)}^2& =\alpha {\cos }^2\theta +\beta (1+\sin \theta {)}^2\\ & =\alpha (1-{\sin }^2\theta )+\beta (1+2\sin \theta +{\sin }^2\theta )\\ & =(\beta -\alpha ){\sin }^2\theta +2\beta \sin \theta +(\beta +\alpha )\end{array}$$

となる。次にこれを$t:=\sin \theta$ としてこれを $t$ の関数

$$\begin{array}{r}f(t):=(\beta -\alpha )t^2+2\beta t+(\beta +\alpha )\end{array}$$

とする。$\theta$ が $0\leqq \theta <2\pi$ の範囲を動くとき，$t$ のとりうる値の範囲は $-1\leqq t\leqq 1$ であるから，$C$ が $D$ に含まれることは，$-1\leqq t\leqq 1$ における $f(t)$ の最大値が $1$ 以下であることと必要十分であり，以下その条件を考える。ただし，$-1\leqq t\leqq 0$ において $f(t)$ は単調に増加することが図よりわかるため，$-1\leqq t\leqq 1$ における $f(t)$ の最大値は $0\leqq t\leqq 1$ におけるそれと同じであり，後者を考えることとする。

(i) $\beta >\alpha$ のとき

$$\begin{array}{r}f(t)=(\beta -\alpha ){(t-\frac{\beta }{\alpha -\beta })}^2+\frac{{\alpha }^2}{\alpha -\beta }\end{array}$$

であり，${\displaystyle \frac{\beta }{\alpha -\beta }}<0$ なので，$f_{\mathrm{m}\mathrm{a}\mathrm{x}}=f(1)=4\beta$ となる。

(ii) $\beta =\alpha$ のとき

$f(t)=2\beta t+(\beta +\alpha )$ より $f_{\mathrm{m}\mathrm{a}\mathrm{x}}=f(1)=4\beta$ である。

(iii) $\beta <\alpha$ のとき

${\displaystyle \frac{\beta }{\alpha -\beta }}\leqq 1(\iff \alpha \leqq 2\beta )$ のときは $f_{\mathrm{m}\mathrm{a}\mathrm{x}}=f(1)=4\beta$ となる。
${\displaystyle \frac{\beta }{\alpha -\beta }}>1(\iff \alpha >2\beta )$ のときは $f_{\mathrm{m}\mathrm{a}\mathrm{x}}=f\left({\displaystyle \frac{\beta }{\alpha -\beta }}\right)={\displaystyle \frac{{\alpha }^2}{\alpha -\beta }}$ となる。

以上より

$$\begin{array}{r}f(t)\mathrm{の}\mathrm{最}\mathrm{大}\mathrm{値}=\{\begin{array}{l}4\beta (\alpha \leqq 2\beta \mathrm{の}\mathrm{と}\mathrm{き})\\ {\displaystyle \frac{{\alpha }^2}{\alpha -\beta }}(\alpha >2\beta \mathrm{の}\mathrm{と}\mathrm{き})\end{array}\end{array}$$

とわかる。この最大値が $1$ 以下であるための正の実数 $\alpha ,\beta$ の条件は

$$\begin{array}{r}\{\begin{array}{l}\alpha \leqq 2\beta \\ 4\beta \leqq 1\end{array}\mathrm{ま}\mathrm{た}\mathrm{は}\{\begin{array}{l}\alpha >2\beta \\ \beta \leqq -{\alpha }^2+\alpha \end{array}\end{array}$$

であり，図示すると次図の色をつけた部分のようになる。境界については，$\alpha$ 軸および $\beta$ 軸上の点をすべて除き，それ以外の点を全て含む。(以下，この領域を $A$ とする。)

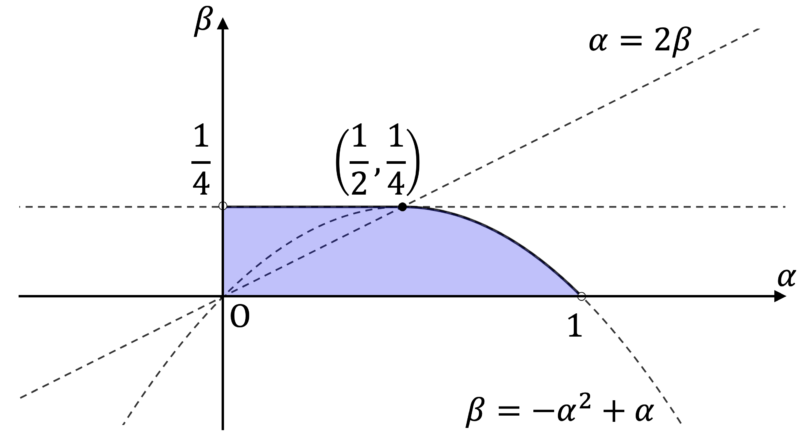
(2)

この楕円の面積は $\pi \sqrt{\alpha \beta }$ であるため，$A$ 内における $\alpha \beta$ の最大点を考えればよい。

$\alpha \beta =k(k:\mathrm{定}\mathrm{数})$ という曲線は，$x$ 軸および $y$ 軸を漸近線にもつ直角双曲線であり，これが $A$ と共有点をもつときの $k$ の最大値を求めるには，曲線 $\alpha \beta =k$ が $A$ の境界のうち $\beta =-{\alpha }^2+\alpha ({\displaystyle \frac{1}{2}}\leqq \alpha <1)$ の部分のみ考えればよい。これは，$\beta ={\displaystyle \frac{1}{4}}$ の部分では $\beta$ が一定であり，$\alpha$ が大きいほど $\alpha \beta$ は大きくなることによる。

曲線 $\alpha \beta =k$ 上の点 $(t,{\displaystyle \frac{k}{t}})({\displaystyle \frac{1}{2}}\leqq t<1)$ における接線の傾きは $-{\displaystyle \frac{k}{t^2}}$ であり，曲線 $\beta =-{\alpha }^2+\alpha$ 上の点 $(t,-t^2+t)$ における接線の傾きは $-2t+1$ である。2 つの曲線が接するための条件は

$$\begin{array}{r}\frac{k}{t}=-t^2+t\mathrm{か}\mathrm{つ}-\frac{k}{t^2}=-2t+1\end{array}$$

であり，これより $t={\displaystyle \frac{2}{3}},k={\displaystyle \frac{4}{27}}$ を得る。この $k$ の値が $\alpha \beta$ の最大値であるため，楕円の面積の最大値は $\pi \sqrt{{\displaystyle \frac{4}{27}}}={\displaystyle \frac{2\pi }{3\sqrt{3}}}$ と求められる。

---

問 題 2 の ポ イ ン ト ・ 補 足

(1) では楕円が円に含まれる条件を求めました。
感覚的には "$\beta$ が小さければ大丈夫そう" なのですが，$\alpha ,\beta$ の条件を正しく求めるためには，方程式の解などの議論に落とし込む必要があります。

(2) では，条件をみたす範囲内で $\alpha \beta$ の範囲を考えました。
(1) でせっかく領域の図示をしたので，それを利用して図形的に $\alpha \beta$ の範囲を求める解法を紹介しました。
あくまで個人的な感想ですが，領域図示を要求されたあとの最大値・最小値問題では，このように図形的なアプローチをしてもよいものと思われます。

---

問 題 3

正の実数 $a$ に対して，座標平面上で次の放物線を考える。

$$\begin{array}{r}C:y=a{x}^2+\frac{1-4a^2}{4a}\end{array}$$

$a$ が正の実数全体を動くとき，$C$ の通過する領域を図示せよ。

2015年 東大 理系数学 第1問

---

問 題 3 の 解 答

$C$ の方程式は $4(x^2-1)a^2-4ya+1=0$ と書き換えられる。これを $a$ の方程式とみたときに，これが正の実数解をもつような $x,y$ の範囲を考える。なお，この方程式の左辺を $f(a)$ とする。

(i) $|x|=1$ のとき $f(a)=-4ya+1$ であり，これが正の実数解をもつ条件は $y>0$ である。

(ii) $|x|>1$ のとき，$f(a)$ は $2$ 次の係数が正の $2$ 次関数である。$f(0)=1>0$ であることも踏まえると，方程式 $f(a)=0$ が正の実数解をもつための条件は

$$\begin{array}{rl}& \{\begin{array}{l}(f(a)\mathrm{が}\mathrm{最}\mathrm{大}\mathrm{と}\mathrm{な}\mathrm{る}a\mathrm{の}\mathrm{値})>0\\ (\mathrm{方}\mathrm{程}\mathrm{式}f(a)=0\mathrm{の}\mathrm{判}\mathrm{別}\mathrm{式}\mathrm{の}\mathrm{値})\geqq 0\end{array}\\ & \iff \{\begin{array}{l}{\displaystyle \frac{y}{2(x^2-1)}}>0\\ {(-4y)}^2-4\cdot 4(x^2-1)\cdot 1\geqq 0\end{array}\\ & \iff \{\begin{array}{l}y>0\\ x^2-y^2\geqq 1\end{array}\end{array}$$

である。

(iii) $(0\leqq )|x|<1$ のとき，$f(a)$ は $2$ 次の係数が負の $2$ 次関数である。$f(0)=1>0$ であることも踏まえると，このとき方程式 $f(a)=0$ は必ず正の実数解をもつ。

以上より，方程式 $f(a)=0$ が正の実数解をもつ条件は

$$\begin{array}{r}\{\begin{array}{l}|x|=1\\ y>0\end{array}\mathrm{ま}\mathrm{た}\mathrm{は}\{\begin{array}{l}|x|>1\\ x^2-y^2\geqq 1\end{array}\mathrm{ま}\mathrm{た}\mathrm{は}(0\leqq )|x|<1\end{array}$$

であり，これを図示すると次の通り。(図には，いくつかの $a$ の値に対応する放物線も描いています。)

---

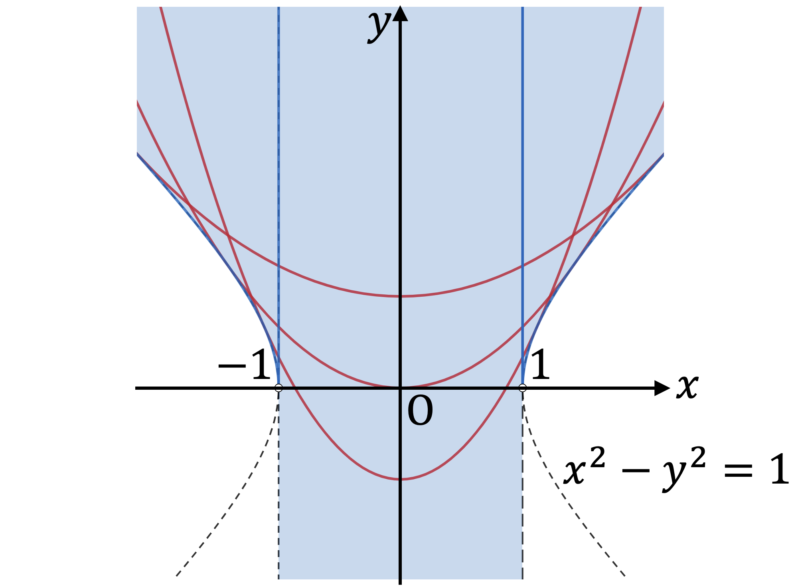
問 題 3 の ポ イ ン ト ・ 補 足

いわゆる逆像法で問題を解きました。放物線の方程式は本来 $xy$ 平面での $x$ と $y$ の関係を表すものですが，これを $a$ の方程式と捉えるのがポイントです。
これは，軌跡・領域問題を攻略するうえで重要なテクニックのひとつです。
ただし，なんでもかんでも逆像法で解ける or 解いた方がいいわけではないので注意してください。

---

参考問題

問題3 と同じように，軌跡を求めた結果 $2$ 次曲線が登場する問題をひとつ載せておきます。

座標平面上の $1$ 点 $\mathrm{P}({\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{4}})$ をとる。放物線 $y=x^2$ 上の $2$ 点 $\mathrm{Q}(\alpha ,{\alpha }^2),\mathrm{R}(\beta ,{\beta }^2)$ を，3 点 $\mathrm{P},\mathrm{Q},\mathrm{R}$ が $\mathrm{Q}\mathrm{R}$ を底辺とする二等辺三角形となるように動かすとき，$\mathrm{△}\mathrm{P}\mathrm{Q}\mathrm{R}$ の重心 $\mathrm{G}(X,Y)$ の軌跡を求めよ。

2011年 東大 文理共通問題

---

ま と め 〜 二 次 曲 線 の 傾 向 〜

$2$ 次曲線そのものの性質を扱った問題は，東大理系数学ではかなり珍しいです。
ただし，$2$ 次曲線が登場していたり，軌跡を求めた結果 $2$ 次曲線が出現したりする問題自体は案外多いです。
したがって，二次曲線自体の問題演習は優先度が低いですが，方程式が与えられたときに速やかにグラフを描けるように対策しておきましょう。

参考問題として 2011 年の文理共通問題を挙げましたが，ほかにも 2019 年度の理系数学第 6 問，2020 年度の理系数学第 6 問などで二次曲線が出現します。
興味のある人は調べてみてください。