【東大数学分野別解説】#14 アプローチが分かれやすい "ベクトル"

文系でも理系でも "ベクトル" は入試の範囲となります。
どういうわけか，図形が絡む分野は苦手とする受験生は多い印象で，差がつく分野といえるでしょう。
というわけで今回は，ベクトルの問題をピックアップします。

---

問 題 1

$\triangle {\rm ABC}$ において $\angle {\rm BAC} = 90^{\circ}, \, \left| \overrightarrow{{\rm AB}} \right|, \, \left| \overrightarrow{{\rm AC}} \right| = \sqrt{3}$ とする。$\triangle {\rm ABC}$ の内部の点 ${\rm P}$ が

$$
\begin{align}
\frac{ \overrightarrow{{\rm PA}} }{\left| \overrightarrow{{\rm PA}} \right|} + \frac{ \overrightarrow{{\rm PB}} }{\left| \overrightarrow{{\rm PB}} \right|} + \frac{ \overrightarrow{{\rm PC}} }{\left| \overrightarrow{{\rm PC}} \right|} = \overrightarrow{0}
\end{align}
$$

を満たすとする。

(1) $\angle {\rm APB}, \, \angle {\rm APC}$ を求めよ。

(2) $\left| \overrightarrow{{\rm PA}} \right|, \, \left| \overrightarrow{{\rm PB}} \right|, \, \left| \overrightarrow{{\rm PC}} \right|$ を求めよ。

---

問 題 1 の 解 答

(1)

$\dfrac{ \overrightarrow{{\rm PA}} }{\left| \overrightarrow{{\rm PA}} \right|}, \, \dfrac{ \overrightarrow{{\rm PB}} }{\left| \overrightarrow{{\rm PB}} \right|}, \, \dfrac{ \overrightarrow{{\rm PC}} }{\left| \overrightarrow{{\rm PC}} \right|}$ はいずれも単位ベクトルである。また，$3$ 点 ${\rm A, \, B, \, C}$ が三角形をなすことから，これら $3$ つのベクトルが "どの $2$ つも互いに平行" となることはない。

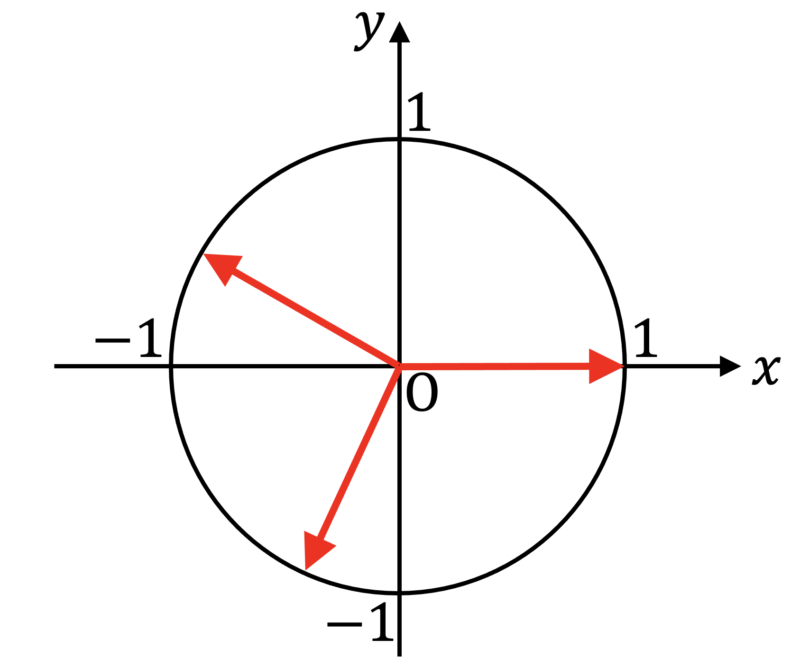
一般に，$3$ つの単位ベクトルの和が $\overrightarrow{0}$ である場合を考える。図のように，$3$ つのうち $1$ つが $(1, \, 0)$ となるように座標平面に配置することができる。$3$ つのベクトル和が $\overrightarrow{0}$ であるため，残りの $2$ つのベクトルの $y$ 成分は打ち消し合うから，これらは $0 < \alpha < \pi$ なる角 $\alpha$ を用いて

$$
\begin{align}
\left( \cos \alpha, \, \sin \alpha \right), \quad \left( \cos \alpha, \, - \sin \alpha \right)
\end{align}
$$

と書くことができる。以上 $3$ つのベクトルは $x$ 成分の和も $0$ であるから，$1 + \cos \alpha + \cos \alpha = 0$ より $\cos \alpha = - \dfrac{1}{2}$ つまり $\alpha = \dfrac{2}{3} \pi$ が成り立つ。以上より，$3$ つの単位ベクトルはどの $2$ つも $120^{\circ}$ の角をなす。

よって $\underline{\angle {\rm APB} = \angle {\rm APC} = 120^{\circ}}$ である。

(2)

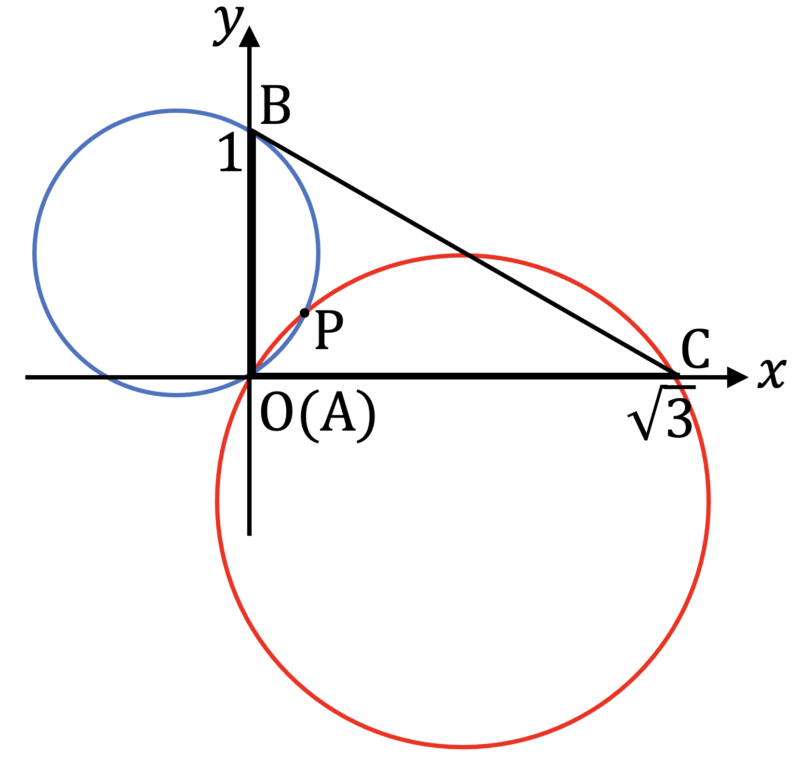
$\angle {\rm AXB} = 120^{\circ}$ をみたす点 ${\rm X}$ の軌跡は図のように青色の円となる。同様に，$\angle {\rm AYB} = 120^{\circ}$ をみたす点 ${\rm Y}$ の軌跡は図のように赤色の円となる。

青色の円は中心 $\left( - \dfrac{1}{2 \sqrt{3}} , \, \dfrac{1}{2} \right)$ であり，半径は $\dfrac{1}{\sqrt{3}}$ であるため，この円の方程式は $\left( x + \dfrac{1}{2 \sqrt{3}} \right)^2 + \left( y - \dfrac{1}{2} \right)^2 = \dfrac{1}{3}$ である。一方，赤色の円は中心 $\left( \dfrac{\sqrt{3}}{2} , \, - \dfrac{1}{2} \right)$ であり，半径は $1$ であるため，この円の方程式は $\left( x - \dfrac{\sqrt{3}}{2} \right)^2 + \left( y + \dfrac{1}{2} \right)^2 = 1$ である。

これら $2$ 円の交点のうち原点でないものが点 $P$ である。$2$ 式を連立すると $y = \dfrac{2}{\sqrt{3}} x$ となり，これと円の方程式を用いることで，原点でない方の交点は $\left( \dfrac{\sqrt{3}}{7}, \, \dfrac{2}{7} \right)$ となる。したがって

$$
\begin{align}
\left| \overrightarrow{{\rm PA}} \right| &= \sqrt{\left( \dfrac{\sqrt{3}}{7} - 0 \right)^2 + \left( \dfrac{2}{7} - 0 \right)^2} = \underline{\dfrac{1}{\sqrt{7}}} \\
\left| \overrightarrow{{\rm PB}} \right| &= \sqrt{\left( \dfrac{\sqrt{3}}{7} - 0 \right)^2 + \left( \dfrac{2}{7} - 1 \right)^2} = \underline{\dfrac{2}{\sqrt{7}}} \\
\left| \overrightarrow{{\rm PC}} \right| &= \sqrt{\left( \dfrac{\sqrt{3}}{7} - \sqrt{3} \right)^2 + \left( \dfrac{2}{7} - 0 \right)^2} = \underline{\dfrac{4}{\sqrt{7}}} \\
\end{align}
$$

となる。

---

問 題 1 の ポ イ ン ト ・ 補 足

初見だと問題文の条件式は扱いにくいかもしれません。あるベクトルをそのベクトルの長さで割ったものは，向きを保った単位ベクトルになるというのがポイントです。正射影を学習している人はすぐ気づけるでしょうが，気づかない人も多い印象です。
$3$ つの単位ベクトルの和が $\overrightarrow{0}$ であるというのは思いのほか強い条件で，これだけで $3$ つのベクトルのなす角を決定できます。解説のように $1$ つのベクトルを $(1, \, 0)$ にするなど，対称性を利用して自由度を減らすことで，議論が楽になります。

(1) ができれば (2) はさほど苦労しないでしょう。実際の試験でも扱いやすい解法を紹介しましたが，ほかにも色々な求め方があるかもしれません。ぜひ考えてみてください。

なお，本問の点 ${\rm P}$ は Fermat 点とよばれる点です。Fermat 点とは，三角形の周または内部にある点であって，各頂点までの距離の合計 ${\rm PA + PB + PC}$ が最小となる点のことです。

---

問 題 2

${\rm O}$ を原点とする座標平面において，点 ${\rm A}(2, \, 2)$ を通り，線分 ${\rm OA}$ と垂直な直線を $l$ とする。座標平面上を点 ${\rm P}$ が次の $2$ つの条件をみたしながら動く。

条件１：
$8 \leqq \overrightarrow{{\rm OA}} \cdot \overrightarrow{{\rm OP}} \leqq 17$

条件２：
点 ${\rm O}$ と直線 $l$ の距離を $c$ とし，点 ${\rm P} (p, \, q)$ と直線 $l$ の距離を $d$ とするとき $cd \geqq (p-1)^2$

このとき点 ${\rm P}$ が動く領域を $D$ とする。さらに，$x$ 軸の正の部分と線分 ${\rm OP}$ のなす角を $\theta$ とする。

(1) $D$ を図示し，その面積を求めよ。

(2) $\cos \theta$ のとりうる値の範囲を求めよ。

2019年 東大 文系数学 第2問

---

問 題 2 の 解 答

(1)

条件１は $8 \leqq 2p + 2q \leqq 17$ つまり $4 \leqq p + q \leqq \dfrac{17}{2}$ と書ける。また，原点と直線 $l$ の距離は $2 \sqrt{2}$ なので $c = 2 \sqrt{2}$ であり，点 ${\rm P}$ と直線 $l$ の距離は

$$
\begin{align}
d = \frac{\left| p + q - 4 \right|}{\sqrt{1^2 + 1^2}} = \frac{\left| p + q - 4 \right|}{\sqrt{2}}
\end{align}
$$

であるため，条件２は

$$
\begin{align}
&{} 2 \sqrt{2} \cdot \frac{\left| p + q - 4 \right|}{\sqrt{2}} \geqq \left( p - 1 \right)^2 \\
&{} \hspace{20mm} \left( \Leftrightarrow 2 \left| p + q - 4 \right| \geqq (p-1)^2 \quad \cdots (\ast) \right)
\end{align}
$$

と求められる。条件１が成り立っているとき $p + q - 4 \geqq 0$ であるため，$( \ast )$ は

$$
\begin{align}
&{} 2(p+q-4) \geqq (p-1)^2 \\
&{} \hspace{20mm} \left( \Leftrightarrow q \geqq \frac{1}{2} p^2 - 2p + \frac{9}{2} \right)
\end{align}
$$

と整理できる。以上より，求める領域を表す不等式は

$$
\begin{align}
\begin{cases}
4 \leqq p+q \leqq \dfrac{17}{2} \\
q \geqq \dfrac{1}{2} p^2 - 2p + \dfrac{9}{2}
\end{cases}
\end{align}
$$

であり，これを図示すると次図の色の濃い部分のようになる。

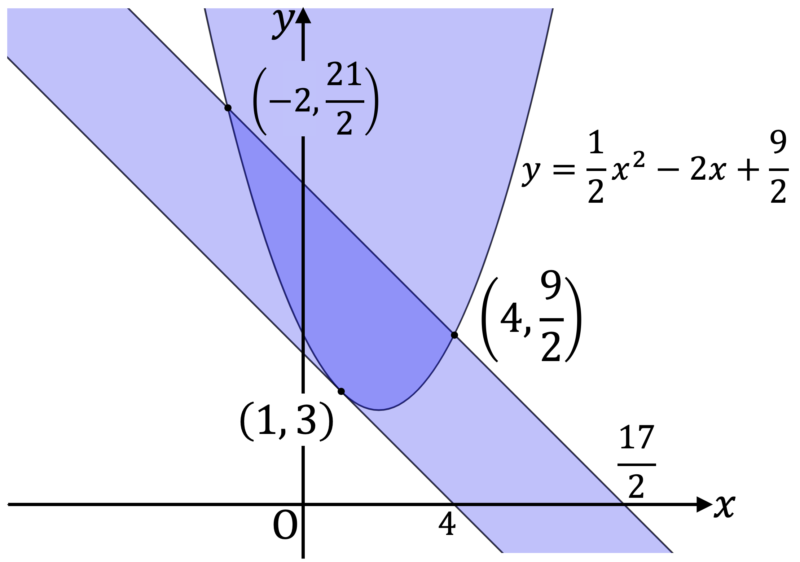
そして，この領域 $D$ の面積は

$$
\begin{align}
&{} \int_{-2}^{4} \left\{ \left( \frac{17}{2} - x \right) - \left( \frac{1}{2} x^2 - 2x + \frac{9}{2} \right) \right\} \, dx \\
&= \int_{-2}^{4} \left( - \frac{1}{2} x^2 + x + 4 \right) \, dx \\
&= \int_{-2}^{4} - \frac{1}{2} (x+2)(x-4) \, dx \\
&= \frac{1}{6} \cdot \frac{1}{2} \cdot \left( 4 - (-2) \right)^3 = \underline{18}
\end{align}
$$

と計算できる。

(2)

放物線 $y = \dfrac{1}{2} x^2 - 2x + \dfrac{9}{2}$ 上の点 $\left( t, \, \dfrac{1}{2} t^2 - 2t + \dfrac{9}{2} \right)$ における接線の方程式を求めると

$$
\begin{align}
&{} y - \left( \frac{1}{2} t^2 - 2t + \frac{9}{2} \right) = (t-2) \left( x - t \right) \\
&{} \left( \Leftrightarrow y = (t-2) x + \left( - \frac{1}{2} t^2 + \frac{9}{2} \right) \right)
\end{align}
$$

となり，これが原点を通るときの $t$ の値は $t = \pm 3$ である。また，対応する接点は $(3, \, 3)$ および $(-3, 15)$ であって，接線の傾きはそれぞれ $1, \, -5$ である。点 $(3, \, 3)$ は $D$ 上にあり，点 $(-3, \, 15)$ は $D$ 上にないことに注意する。

一方，原点と点 $\left( 4, \, \dfrac{9}{2} \right)$ を通る直線の傾きは $\dfrac{9}{8}$ であり，原点と点 $\left( -2, \, \dfrac{21}{2} \right)$ を通る直線の傾きは $- \dfrac{21}{4}$ となっている。

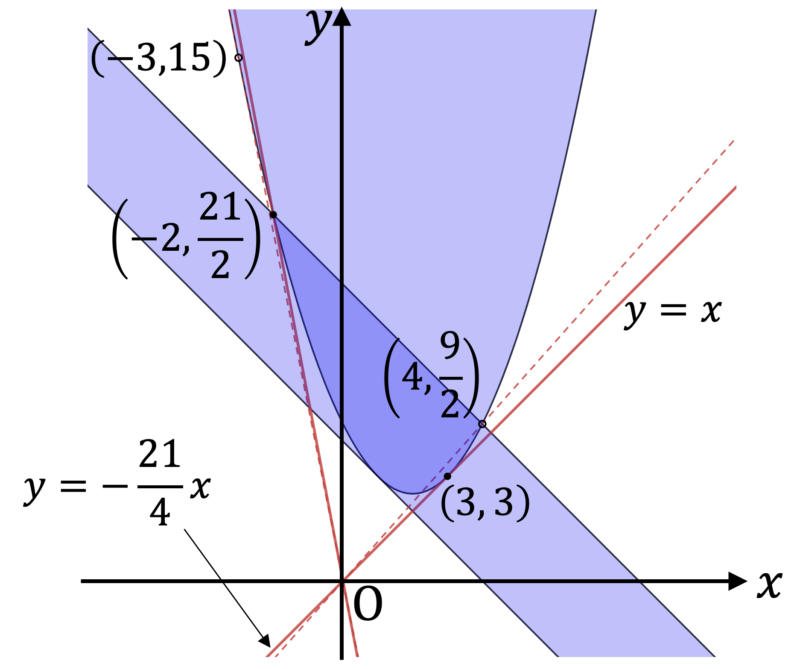
以上より $\tan \theta$ のとりうる値の範囲は $- \dfrac{21}{4} \leqq \tan \theta \leqq 1$ であり，これを $\cos$ になおすと

$$
\begin{align}
\underline{- \frac{4}{\sqrt{457}} \leqq \cos \theta \leqq \frac{\sqrt{2}}{2}}
\end{align}
$$

となる。

---

問 題 2 の ポ イ ン ト ・ 補 足

問題文にベクトルが登場していますが，すぐに $p, \, q$ に関する不等式に直すことができます。それができたら，もはやベクトルの問題ではありません。
(2) では $\cos \theta$ の値が問われていますが，一旦 $\tan$ の値の範囲を求めると明快です。$\tan$ の範囲がもとまったら，それを $\cos$ の範囲に直せばクリアです。

---

問 題 3

${\rm O}$ を原点とする座標平面を考える。不等式

$$
\begin{align}
|x| + |y| \leqq 1
\end{align}
$$

が表す領域を $D$ とする。また，点 ${\rm P, \, Q}$ が領域 $D$ を動くとき，$\overrightarrow{{\rm OR}} = \overrightarrow{{\rm OP}} - \overrightarrow{{\rm OQ}}$ をみたす点 ${\rm R}$ が動く範囲を $E$ とする。

(1) $D, \, E$ をそれぞれ図示せよ。

(2) $a, \, b$ を実数とし，不等式

$$
\begin{align}
|x-a| + |y-b| \leqq 1
\end{align}
$$

が表す領域を $F$ とする。また，点 $S, \, T$ が領域 $F$ を動くとき，$\overrightarrow{{\rm OU}} = \overrightarrow{{\rm OS}} - \overrightarrow{{\rm OT}}$ をみたす点 ${\rm U}$ が動く範囲を $G$ とする。$G$ は $E$ と一致することを示せ。

2019年度 東大 文系数学 第4問

---

問 題 3 の 解 答

(1)

$|x| + |y| = 1$ なる実数の組 $(x, \, y)$ について，$x$ の符号を自由に変えてもやはり $|x| + |y| = 1$ は成り立つし，$y$ についても同様である。したがってこの図形は $x$ 軸対称かつ $y$ 軸対称である。

$x \geqq 0, \, y \geqq 0$ の範囲において，この方程式は $2$ 点 $(1, \, 0), \, (0, \, 1)$ を結ぶ線分を表す。よって $D$ を図示すると，次図の色をつけた部分のようになる。なお，境界はすべて $D$ に含まれる。

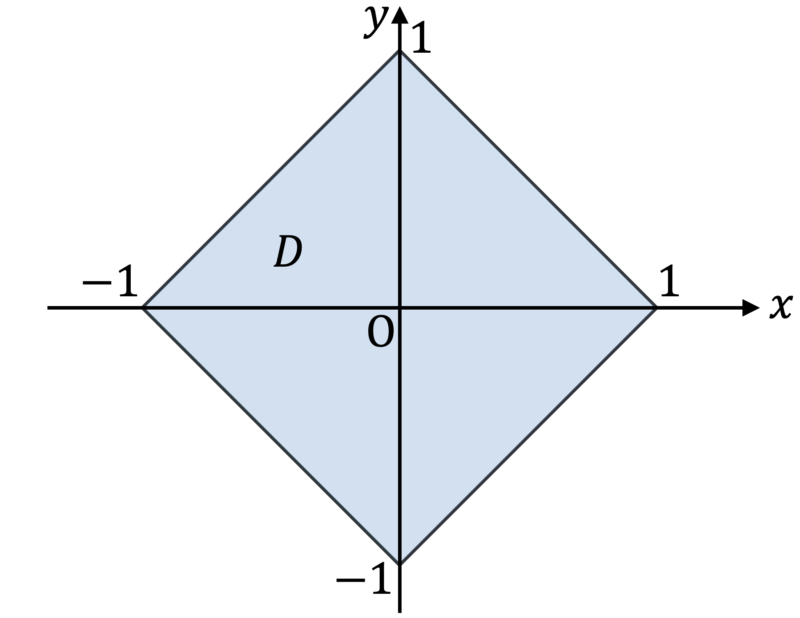
次に $E$ を求める。点 ${\rm Q}$ が領域 $D$ を動くとき，$\overrightarrow{{\rm OQ'}} = - \overrightarrow{{\rm OQ}}$ をみたす点 ${\rm Q'}$ が動く領域は $D$ をなすすべての点を原点中心に対称移動した点の集合であるが，これは $D$ そのものである。よって $\overrightarrow{{\rm OR}} = \overrightarrow{{\rm OP}} - \overrightarrow{{\rm OQ}} = \overrightarrow{{\rm OP}} + \overrightarrow{{\rm OQ'}}$ をみたす点 ${\rm R}$ が動く範囲 $E$ は，領域 $D$ の形をした正方形の中心が領域 $D$ を動くときに，その正方形の周および内部が通過する領域となる。これを図示すると，次図の色をつけた部分のようになる（点線部およびその内部は $D$ である）。なお，境界はすべて $E$ に含まれる。

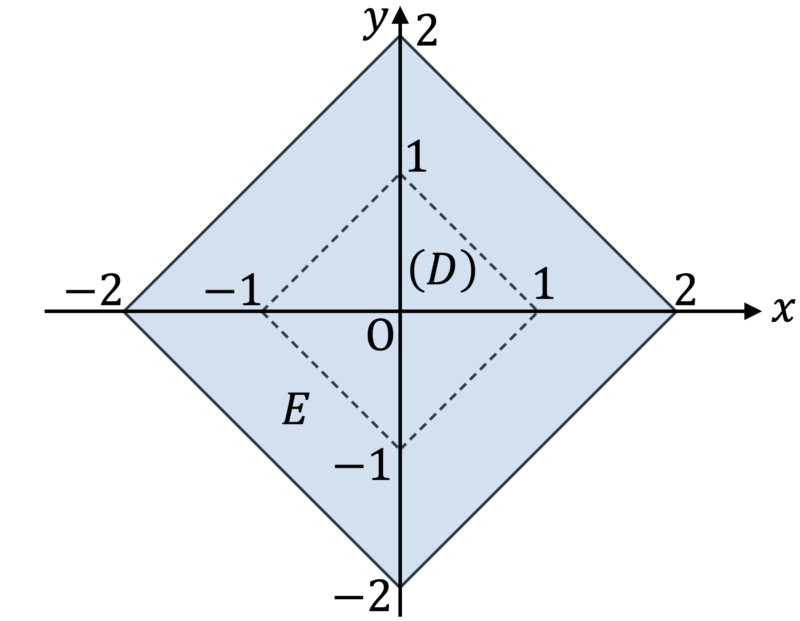
(2)

点 $(X, \, Y)$ が領域 $E$ 内にあるとする。これはたとえば $\overrightarrow{{\rm OP}} = \left( \dfrac{X}{2}, \, \dfrac{Y}{2} \right), \, \overrightarrow{{\rm OQ}} = \left( - \dfrac{X}{2}, \, - \dfrac{Y}{2} \right)$ に対応している（このような点 ${\rm P, \, Q}$ はいずれも $D$ に属する）。ここで $\overrightarrow{{\rm OS}} = \left( a + \dfrac{X}{2}, \, b + \dfrac{Y}{2} \right), \, \overrightarrow{{\rm OT}} = \left( a - \dfrac{X}{2}, \, b - \dfrac{Y}{2} \right)$ とすれば，これらは $F$ に属しており，$\overrightarrow{{\rm OU}} = (X, \, Y)$ となる。これは領域 $E$ 内の任意の点 $(X, \, Y)$ に対していえるため，$E \subset G$ がいえる。

次に，点 $(X, \, Y)$ が領域 $G$ 内にあるとする。このとき，ある実数の組 $(p, \, q)$ が存在して $\overrightarrow{{\rm OS}} = \left( p + X, \, q + Y \right), \, \overrightarrow{{\rm OT}} = \left( p, \, q \right)$ と書くことができ，これらをみたす点 ${\rm S, \, T}$ は $F$ に属する。領域 $F$ は領域 $D$ を $x$ 軸方向に $a$，$y$ 軸方向に $b$ だけ平行移動したものであるから，点 ${\rm S, \, T}$ をこれと逆に移動した点 $\left( p + X - a, \, q + Y - b \right), \, \left( p - a, \, q - b \right)$ は $D$ に属する。点 ${\rm P, \, Q}$ をそれらの点とすることで，

$$
\begin{align}
\overrightarrow{{\rm OR}} &= \overrightarrow{{\rm OP}} - \overrightarrow{{\rm OQ}} \\
&= \left( p + X - a, \, q - Y - b \right) - \left( p - a, \, q - b \right) \\
&= (X, \, Y)
\end{align}
$$

となるため，$G \subset E$ がいえる。

以上より $E \subset G$ かつ $G \subset E$ であるため，$E$ と $G$ は一致する。■

---

問 題 3 の ポ イ ン ト ・ 補 足

(1) のように，ベクトルの終点の存在範囲を図示する問題は，近年の東大数学において文理問わず頻出です。本問のほかには，たとえば 2021 年度の理系数学第 2 問があります。

(2) はさまざまな説明方法があると思いますが，解説では $E$ が $G$ に含まれること，$G$ が $E$ に含まれることの双方をいうことにより $E = G$ であることを示しました。この結果を端的に述べると，点 $U$ の存在領域に影響するのはあくまで点 ${\rm S, \, T}$ の相対位置であって，これらの存在範囲全体が $x$ 軸方向に $a$，$y$ 軸方向に $b$ 平行移動したところでそれは変化しないというわけです。興味のある人は，点 ${\rm S}$ の動く範囲のみが $F$ であったり，逆に点 ${\rm T}$ の動く範囲のみが $F$ であったりする場合の点 $U$ の存在領域を考えてみてください。

---

ま と め

東大数学の中から，ベクトルが登場する問題を 3 つピックアップしました。
ただ，内積や垂心の位置，三角形の面積を求めるといったド定番の問題ではなく，あえてちょっとずれた問題ばかりにしてみました。

問題 1 のように平面図形の点の位置を決定するのに用いることもあれば，問題 2 のようにすぐにベクトルが消えてしまうこともあり，そして問題 3 のように点の存在領域を求めるためにフル活用することもあります。

使えるときはフル活用し，他の手段が優れているときはさっさとそれに移行する，という使い分けが大切です。
微分や積分などと異なり "とりあえずこれをこうやって計算すればいいんだよ" というモノが与えられていないのが図形問題の難しいところであり，また魅力でもあります。
たくさん問題演習を重ね，適切なアプローチをとれるようにしましょう！