【東大数学分野別解説】#01 定番の "確率漸化式"

2021.12.07

この連載では，東大数学の過去問の中から学びの多そうなものを分野別に解説していきます。単に正解を述べるだけでなく，問題を解く際のアプローチや補足事項も添えるので，初見の問題への対応力も磨けることでしょう。

分野別過去問解説の第 1 弾。
今回は確率分野から 2 問ピックアップします！

問題 1

まずは 2012 年度の文理共通問題です。有名な問題なので，知っている人も多いはず。

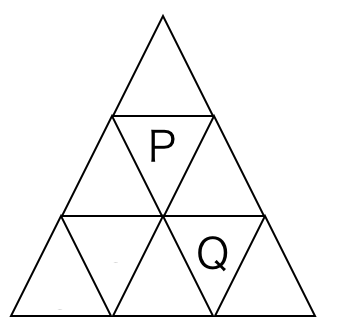
図のように，正三角形を 9 つの部屋に辺で区切り，部屋 ${\rm P, \, Q}$ を定める。1 つの球が部屋 ${\rm P}$ を出発し，1 秒ごとに，そのままその部屋にとどまることなく，辺を共有する隣の部屋に等確率で移動する。球が $n$ 秒後に部屋 ${\rm Q}$ にある確率を求めよ。
東京大学 2012年度理系数学第2問, 文系数学第3問

解答を見る前に，一旦自身でよく考えてみましょう。
初見の問題への対応力も，入試では大切ですからね。

問題 1 の解答

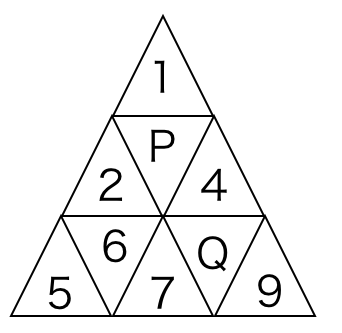
図のように各部屋に番号をつける。$n$ 秒後に部屋 ${\rm Q}$ にいる確率を $p(n)$ とおく。${\rm P}$ から奇数回の移動後には必ず $1, \, 2, \, 4, \, 5, \, 7, \, 9$ のいずれかにいて，偶数回の移動後には必ず ${\rm P}, \, 6, \, {\rm Q}$ のいずれかにいることに注意する。

よって $n$ が奇数のとき $p(n)=0$ である。

以下，$n$ が偶数のときを考える。対称性より $n$ 秒後に部屋 $6$ にいる確率は $p(n)$ となる。また，余事象の考え方から$n$ 秒後に部屋 $P$ にいる確率は $1-2p(n)$ となる。

次に $p(n)$ と $p(n-2)$ の間の関係式を作る。$n$ 秒後に部屋 ${\rm Q}$ にいるのは，以下の 3 パターンのいずれかに場合分けできる：

$(n-2)$ 秒後に部屋 ${\rm P}$ にいて，そこから ${\rm P} \to 4 \to {\rm Q}$ と移動する
$(n-2)$ 秒後に部屋 $6$ にいて，そこから $6 \to 7 \to {\rm Q}$と移動する
$(n-2)$ 秒後に部屋 ${\rm Q}$ にいて，そこから ${\rm Q} \to (4 \, {\rm or} \, 7 \, {\rm or} \, 9) \to {\rm Q}$ と移動する

よって，

$$
\begin{align}
p(n) &= (1-2p(n-2)) \cdot \displaystyle\frac{1}{3}\cdot\frac{1}{2} \\
&\hspace{10mm} + p(n-2) \cdot \frac{1}{3} \cdot \frac{1}{2} \\
&\hspace{10mm} + p(n-2) \cdot \frac{1}{3} \left( \frac{1}{2} + \frac{1}{2} + 1 \right)
\end{align}
$$

これを整理すると，

$p(n) = \displaystyle\frac{1}{2} p(n-2)+ \displaystyle\frac{1}{6}$

これは単純な二項間漸化式である。特性方程式の解が1/3であることに注意すると，

$p(n) - \displaystyle\frac{1}{3} = \frac{1}{2} \left( p(n-2)-\frac{1}{3} \right)$

と変形できる。これと初期条件 $p(0)=0$ より，$p(n) = \underline{\displaystyle\frac{1}{3} \left( 1-2^{-\frac{n}{2}} \right)}$ を得る。

問題 1 のポイント・補足

漸化式を立て確率を求めるという頻出問題です。
$n$ の偶奇で分けて考える，対称性に注目することで変数の数を減らす（単純な 2 項間漸化式を導く）というのがポイントです。
$n$ が十分大きいとき部屋 ${\rm P}, \, 6, {\rm Q}$ にいる確率は均等になりそう，つまり $p(n) \to \displaystyle\frac{1}{3}$ と予想できます。実際答えの極限を考えると $\displaystyle\frac{1}{3}$ になることが分かります。このように極限を考えることで検算になります。

問題 2

続いて，1995 年度の文理共通問題です。

サイコロを $n$ 回投げて，$xy$ 平面上の点 ${\rm P}_0, \, {\rm P}_1, \, \cdots, \, {\rm P}_n$を次の規則 (a), (b) によって定める。
(a) ${\rm P}_0=(0,0)$
(b) $1 \leq k \leq n$ のとき，$k$ 回目に出た目の数が $1, \, 2, \, 3, \, 4$ のときには ${\rm P}_{k-1}$ をそれぞれ東，北，西，南に $\displaystyle\frac{1}{2^k}$ だけ動かした点を ${\rm P}_k$ とする。また $k$ 回目に出た目の数が $5, \, 6$ のときには ${\rm P}_k = {\rm P}_{k-1}$ とする。ただし $y$ 軸の正の向きを北と定める。
このとき以下の問に答えよ。
(1) ${\rm P}_n$ が $x$ 軸上にいれば，${\rm P}_0, \, {\rm P}_1, \, \cdots, \, {\rm P}_{n-1}$ もすべて $x$ 軸上にあることを示せ。
(2) ${\rm P}_n$ が第一象限 $\{(x,y\mid x> 0, y > 0)\}$ にある確率を $n$ で表せ。
東京大学 1995年理系数学第5問, 文系数学第3問

問題 2 の解答

(1)

一回 $x$ 軸からはみ出ると戻ってこれないことを証明すればよい。

$k$ 回目ではじめて $x$ 軸からはみ出た場合，$P_k$ の $y$ 座標の絶対値は $\displaystyle\frac{1}{2^k}$ である。
また，$k+1$ 回目から $n$ 回目までの移動距離は最大で，

$\displaystyle\frac{1}{2^{k+1}} + \frac{1}{2^{k+2}} + \cdots + \frac{1}{2^n}$

であり，

$\displaystyle\frac{1}{2^k} - \left( \displaystyle\frac{1}{2^{k+1}} + \frac{1}{2^{k+2}} + \cdots + \frac{1}{2^n} \right) = \frac{1}{2^n} > 0$

未満である。以上より，ある $N \in \mathbb{N}$ に対し ${\rm P}_{N}$ が $x$ 軸上にないとすると，$n > N$ なる任意の正の整数 $n$ に対し ${\rm P}_{n}$ は $x$ 軸上にないため題意がしたがう。

(2)

${\rm P}_n$ が第一象限にある確率を $p_{n}$ とおく。対称性より他の象限にある確率もそれぞれ $p_{n}$ となる。
${\rm P}_n$ が $x$ 軸上にある確率は，(1) より $n$ 回とも 2 と 4 が出ない確率であり，$\left( \displaystyle\frac{4}{6} \right)^n$ である。$y$ 軸上にある確率も同じである。
また，${\rm P}_n$ が原点にある確率は，$n$ 回とも 5 か 6 が出る確率であり $\left( \displaystyle\frac{2}{6} \right)^n$ である。
以上より，$4p_{n} + 2 \left( \displaystyle\frac{2}{3} \right)^n - \left( \displaystyle\frac{1}{3} \right)^n = 1$という式が成り立つ。これを $p_{n}$ について解くと，$p_{n} = \displaystyle\frac{1}{4} \left\{1-2 \left( \frac{2}{3} \right)^n + \left( \frac{1}{3} \right)^n \right\}$ が得られる。

問題 2 のポイント・補足

"確率の総和が $1$ になる" のが (2) のポイントです。
某参考書によると比較的難しい問題とされていますが，考え方はそこまで難しくありません。ひとつずつ丁寧に処理していくのみです。
東大の問題の多くは本問のように "典型的でない・問題文が長め" なので受験生が面食らって平均点が下がりやすいです。このような問題に直面しても動揺せずにに落ち着いて問題文を読むことが重要です。