【東大数学分野別解説】#04 確実に正解したい "微分"

分野別過去問解説の第 4 弾です。
今回は微分（関数の最大値を求める）の問題を 2 問ピックアップしています。
最後に東大数学の微分の問題の特徴，傾向についても述べます！

問 題 1

まずは 2011年 理系 第1問。

---

問題 1 の解答

(1)

直線 $\mathrm{Q}\mathrm{R}$ と $y$ 軸の交点を $\mathrm{A}$ とする。$\mathrm{A}$ の $y$ 座標は $a$ なので $\mathrm{P}\mathrm{A}=1-a$ である。あとは $\mathrm{Q}$ の $x$ 座標 $q_x$ と $\mathrm{R}$ の $x$ 座標 $r_x$ の差を求めればよい。

$q_x,r_x$ は，円の方程式 $x^2+(y-1{)}^2=1$ と直線の方程式 $y=a(x+1)$ から $y$ を消去した $x$ についての方程式の解である。実際に $y$ を消去すると，

$$\begin{array}{r}{x}^2+a^2(x+1{)}^2-2a(x+1)=0\\ (a^2+1)x^2+2(a^2-a)x+a^2-2a=0\end{array}$$

よって，解と係数の関係より，

$q_x+r_x=-{\displaystyle \frac{2(a^2-a)}{a^2+1},q_x{r}_x={\displaystyle \frac{a^2-2a}{a^2+1}}}$

これを用いると，

$|q_x-r_x|=\sqrt{(q_x+r_x{)}^2-4q_x{r}_x}={\displaystyle \frac{2\sqrt{2a}}{a^2+1}}$

以上より求める面積は，

$S(a)={\displaystyle \frac{1-a}{2}\cdot \frac{2\sqrt{2a}}{a^2+1}=\underset{―}{\frac{(1-a)\sqrt{2a}}{a^2+1}}}$

(2)

$S(a)$ を微分すると，

$S^{\prime }(a)={\displaystyle \frac{(a+1)(a-2+\sqrt{3})(a-2-\sqrt{3})}{(a^2+1{)}^2\sqrt{2a}}}$

となる。よって $0<a\le 2-\sqrt{3}$ で $S^{\prime }(a)>0$，$2-\sqrt{3}\le a<1$ で $S^{\prime }(a)<0$ であり，$S(a)$ が最大となるのは $a=\underset{―}{2-\sqrt{3}}$ のときとわかる。

---

問 題 1 の ポ イ ン ト・補 足

• (1) は東大にしては考え方が易しめなので "少々大変でもとにかく計算をやりきること" "結果に自信をもって (2) に進めるように検算をすること" が重要です。
• 検算方法の例として，(1) の答えに $a=0$ や $a=1$ を代入すると $0$ になることが確認できます。
• (2) もただ微分するだけの易問です。$S(a)$ の根号を外すために 2 乗してから微分するという方法もありますが，計算量はほとんど変わりません。
• (2) の答え $2-\sqrt{3}$ はだいたい $0.27$ です。これは直感的にも正しそうな値なので自信をもって次の問題に行けます（もちろん，この辺りの感覚は人によりますが）。

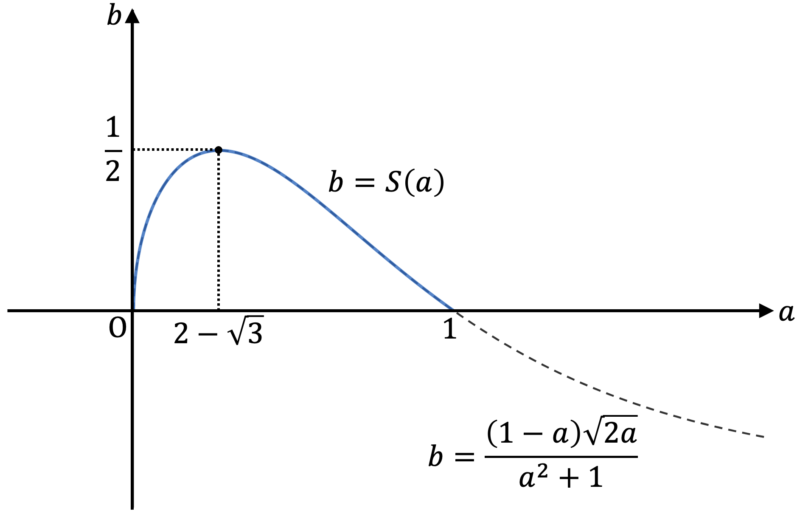
なお，$S(a)$ のグラフは次のようになります。$S(a)$ の最大値は ${\displaystyle \frac{1}{2}}$ です。

---

問 題 2

続いて 1998年 文系 第1問, 理系 第1問（文理共通）。

---

問 題 2 の 解 答

$f(x)$ を微分すると，

$$\begin{array}{rl}{f}^{\prime }(x)& =9x^2-6(a-{\displaystyle \frac{1}{a}})x-4\\ & =(3x-2a)(3x+{\displaystyle \frac{2}{a}})\end{array}$$

よって，極大値と極小値の差は $f\left({\displaystyle \frac{2}{3}a}\right)$ と $f(-{\displaystyle \frac{2}{3a}})$ の差である。計算していくと，

$$\begin{array}{rl}& f\left(\frac{2}{3}a\right)-f(-\frac{2}{3a})\\ & =(\frac{4}{3}{a}^2-4)(\frac{1}{a}-\frac{a}{3})-(\frac{4}{3a^2}-4)(\frac{1}{3a}-a)\\ & =\frac{4}{9a^3}(a^6+3a^4+3a^2+1)\\ & =\frac{4}{9a^3}(a^2+1{)}^3\end{array}$$

となる。$a$ を $-a$ にしても極大値と極小値の差は変わらない。よって，以下 $a$ が正の場合を考える。
相加平均・相乗平均の不等式より

$$\begin{array}{rl}\frac{4}{9a^3}(a^2+1{)}^3& =\frac{4}{9}{(a+\frac{1}{a})}^3\\ & \ge \frac{4}{9}{\left(2\sqrt{a\cdot \frac{1}{a}}\right)}^3\\ & =\frac{32}{9}\end{array}$$

等号成立は $a=1$ のとき。よって答えは $a=\underset{―}{\pm 1}\cdots \mathrm{答}$

---

問 題 2 の ポ イ ン ト ・ 補 足

• これも東大にしてはかなりの易問。計算ミスのないように何度も検算すべき。
• $f^{\prime }(x)=0$ の解を $\alpha ,\beta$とおき，$f(\alpha )-f(\beta )={\displaystyle {\int }_{\beta }^{\alpha }{f}^{\prime }(x)dx}$ を用いて計算することもできる。この方法の方が計算は楽だが，発想力が必要。本番は愚直な方法でも良いから完答することが大切であることは忘れずに！

---

ま と め 〜 東 大 微 分 の 傾 向 〜

• 微分を中心とした問題は易しい問題が多い（一方積分中心の問題は発想，計算ともに難しい問題が多い）。
• ただし，微分の計算自体はかなり複雑な問題もある。発想力では差がつかないことが多く，とにかく計算ミスをしないことが重要。
• 今回の問題 1 のように，前半の小問で図形のとある量を計算させ，後半の小問でその量の最大値（または最小値）を微分を使って求めさせる問題が頻出。