【A級紙】 #06 双曲螺旋の弧長 ～東大入試の積分問題を添えて～

最新の入試数学を追いかけるのもよいですが，たまにはちょっとした昔話を。（といっても，ほぼ現在の大学入試の範囲内です。）

僕が東大を受験した 2015 年度入試から始まった新課程では，新たに “曲線の長さ” が 数学Ⅲ の範囲になりました。
それまでの課程で次の “曲線の長さ（弧長）を求める公式” を明確に入試の出題範囲としていたのは大学は京都大学くらいのものでしたが，いまや次の事実は理系受験生の多くが知っているはずです。

媒介変数 $t$ について微分可能な 2 つの関数 $x(t), \, y(t)$ によって

$x = x(t), \, y = y(t) \quad ( a \leq t \leq b)$

と媒介変数表示される曲線の長さ $s$ は，

$s = \displaystyle\int_{a}^{b} \sqrt{\left( \frac{dx}{dt} \right)^2 + \left( \frac{dy}{dt} \right)^2} \, dt$

と表せる。

媒介変数表示された曲線の長さ

どうしてこうなるかについては，これまでの A級紙 で紹介してきた微分・積分の考え方を理解できている人であれば，次の図が理解しやすいと思います。：

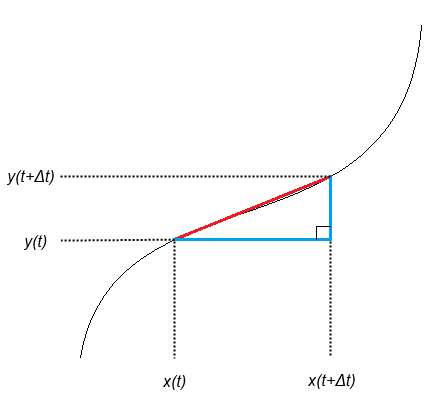
媒介変数 $t \to t + \Delta t$ に対応する曲線上の 2 点を結ぶことを考えます。ここで $\Delta t$ は微小量です。
このとき，図の赤線部の長さを $\Delta s$ とすると

$$
\begin{align}
\Delta s &= \sqrt{ \left( x(t + \Delta t) - x(t) \right)^2 + \left( y(t + \Delta t) - y(t) \right)^2 } \\
&= \sqrt{ \left( \displaystyle\frac{x(t + \Delta t) - x(t)}{\Delta t} \right)^2 + \left( \displaystyle\frac{y(t + \Delta t) - y(t)}{\Delta t} \right)^2 } \Delta t \\
&= a
\end{align}
$$

ここで $\Delta t \to 0$ の極限をとれば赤線の長さは最小となり，ほぼ 2 点間を結ぶ曲線の長さに等しいとみなせるようになるので（ここではそういうことにしましょう），$t = a$ から $t = b$ まで $t$ を連続的に変化させて $\Delta s$ を足し合わせたものが $s$ であると考えれば，さきの公式が得られます。

さて，突然ですが，ここで東大理系数学 2011 年第 3 問を見てみましょう。

$L$ を正定数とする。座標平面の $x$ 軸上の正の部分にある点 ${\rm P}(t, \, 0)$ に対し，原点 ${\rm O}$ を中心とし点 ${\rm P}$ を通る円周上を，${\rm P}$ から出発して反時計回りに道のり $L$ だけ進んだ点を ${\rm Q}\left( u(t), \, v(t) \right)$ と表す。

(1) $u(t), \, v(t)$ を求めよ。

(2) $0 < a < 1$ の範囲の実数 $a$ に対し，積分

$\hspace{10mm} f(a) = \displaystyle\int_{a}^{1} \sqrt{\left\{ u'(t) \right\}^2 + \left\{ v'(t) \right\}^2} \, dt$

　を求めよ。

(3) 極限 $\displaystyle\lim_{a \to +0} \displaystyle\frac{f(a)}{\log a}$ を求めよ。

先ほどの内容を踏まえると，(2) で計算すべき積分値 $f(a)$ が何らかの弧長を表していることは一目瞭然。
とすれば，(3) で計算する極限に何らかの視覚的意味を見出したくなるのは人の性（？）ですね。

問題文にある点 ${\rm Q}$ が媒介変数 $t$ を変化させたときに描く軌跡を "双曲螺旋" といって，このグラフ自体は通常極座標で

$r = \displaystyle\frac{b}{\theta}$

などと表されます。
点 ${\rm Q}$ の軌跡は $\theta \to \displaystyle\frac{L}{t}, \, b = L$ としたものに相等するわけですね。

この双曲螺旋自体は大学入試で別段重要な曲線というわけではありませんが，概形は次のようになっています。：

---

ちょっと話題がそれますが，直前期の理系受験生ならこの軌跡の無限遠での様子を求めてほしいところです。わかりますか？

答え：
極座標表示の式において $\theta \to 0$ とすればよいわけですから，$xy$ 座標に直して簡単な極限計算をすれば，$x \to \infty, \, y \to b$ となります。
この計算は本問の設定に対応付けると $t →∞$ の場合を考えていることになりますが，点 ${\rm Q}$ は “原点を中心とし点 ${\rm P}(t,0)$ を通る円周上を，${\rm P}$ から出発して反時計回りに道のり $L$ だけ進んだ点” だったわけですから，$x \to \infty, \, y \to L$ となるのは妥当に思えますね。

---

さて，話を戻しましょう。(3) の $\displaystyle\lim_{a \to +0} \displaystyle\frac{f(a)}{\log a}$ について考えます。

問題文の情報を整理すると，$f(a)$ は "媒介変数 $t$ を $a \leq t \leq 1$ の範囲で動かしたときの点 ${\rm Q}$ の軌跡（双曲螺旋の一部）の弧長" のことでした。
$t = 1$ に対応するのはどこかの点であって，$t \to +0$ とすると点 ${\rm Q}$ は原点に限りなく近づくことになるのが分かりますから，上図を見れば ${\rm Q}$ が原点の周りをぐるぐる回って弧長 $f(a)$ はどんどん長くなるように見えます（もちろん，弧長 $f(a)$ 自体が収束する可能性も捨てきれませんが）。
対する $\log a$ は $a \to +0$ で $-\infty$ に発散しますから，題意の極限が何らかの負の定数値に収束してもおかしくなさそうです。

結局感覚的な理解はここまでで，答えを知るにはやっぱり計算するしかありません。
しかし，何らかの図形的解釈ができる計算に対し状況をイメージすることは基本的には大切にしたい精神です。

もちろん試験中にここまでやることは要求しませんが，解き終わった後の問題についてぼーっと理解を深めるのもまたよい勉強となります。
実際，サイクロイドが円を転がした時に出てくる軌跡だというのはいろんな参考書に書いてありますが，軌跡としての双曲螺旋が図形的に本問のようにして描かれるというのはなかなかお目にかかれない事実でしょう。

高校数学の "いろいろな曲線" では，教科書にオマケ程度の扱いでも様々な曲線が紹介されています。
東大受験に際してこれらの曲線の名前とその性質を覚えておく必要はほとんどないでしょうが，せめてそういう問題と出会ったときくらいは，特殊な図形的性質を持つ曲線が比較的シンプルな式で表されてしまう面白さを感じることのできる，“とりあえず見てみよう” というその気持ち，無垢な心を忘れたくないものです。
だって東大が本問を本当にただの計算問題として出題したかったのなら，回りくどい問題設定も (1) も必要なかったはずなんですから。

次回は別の曲線を扱います。お楽しみに！

補足：問題の略解と答え

先ほどの東大の過去問，当然ですが答えが気になる人もいることでしょう。
そこで，略解と計算結果を載せておきます。
答えのみ示す箇所もありますが，途中過程は各自で補完してみてください。

(1)

$\underline{u(t) = t \cos \displaystyle\frac{L}{t}, \, v(t) = t \sin \displaystyle\frac{L}{t}} \quad \cdots 答$

(2)

$u'(t) = \cos \displaystyle\frac{L}{t} + \displaystyle\frac{L}{t} \sin \displaystyle\frac{L}{t}, \, v'(t) = \sin \displaystyle\frac{L}{t} - \displaystyle\frac{L}{t} \cos \displaystyle\frac{L}{t}$ であるから

$$
\begin{align}
&{} \left\{ u'(t) \right\}^2 + \left\{ v'(t) \right\}^2 \\
&= \left\{ \cos \displaystyle\frac{L}{t} + \displaystyle\frac{L}{t} \sin \displaystyle\frac{L}{t} \right\}^2 + \left\{ \sin \displaystyle\frac{L}{t} - \displaystyle\frac{L}{t} \cos \displaystyle\frac{L}{t} \right\}^2 \\
&= 1 + \displaystyle\frac{L^2}{t^2}
\end{align}
$$

となり，問題文の積分は

$$
\begin{align}
f(a) = \displaystyle\int_{a}^{1} \sqrt{1 + \displaystyle\frac{L^2}{t^2}} \, dt
\end{align}
$$

と書くことができる。ここで $L = t \tan \theta$ とし，$\tan \theta = \displaystyle\frac{L}{a}$ となる鋭角 $\theta$ の値を $\alpha$，$\tan \theta = L$ となる鋭角 $\theta$ の値を $\beta$ とすると

$$
\begin{align}
f(a) &= \displaystyle\int_{\alpha}^{\beta} \sqrt{1 + \displaystyle\frac{1}{\tan^{2} \theta}} \cdot \left( - \displaystyle\frac{L}{\sin^2 \theta} \right) \, d\theta \\
&= L \displaystyle\int_{\beta}^{\alpha} \displaystyle\frac{1}{\cos\theta \sin^2 \theta} \, d\theta \\
&= L \displaystyle\int_{\beta}^{\alpha} \displaystyle\frac{\cos \theta}{(1 - \sin^2 \theta) \sin^2 \theta} \, d\theta
\end{align}
$$

と変形でき，ここで $u = \cos \theta$ とすることで

$$
\begin{align}
f(a) &= L \displaystyle\int_{\frac{L}{\sqrt{L^2 + 1}}}^{\frac{L}{\sqrt{L^2 + a^2}}} \frac{1}{(1 - u^2)u^2} \, du \\
&= L \displaystyle\int_{\frac{L}{\sqrt{L^2 + 1}}}^{\frac{L}{\sqrt{L^2 + a^2}}} \left\{ \displaystyle\frac{1}{2} \left( \frac{1}{1-u} + \frac{1}{1+u} \right) + \frac{1}{u^2} \right\} \\
&= L \left[ \displaystyle\frac{1}{2} \log \frac{1+u}{1-u} - \frac{1}{u} \right]_{\frac{L}{\sqrt{L^2 + 1}}}^{\frac{L}{\sqrt{L^2 + a^2}}}\\
&= \underline{L \left\{ - \log a + \log \left( \sqrt{L^2 + a^2} + L \right) \right. } \\
&{} \hspace{45mm} \underline{\left. - \log \left( \sqrt{L^2 + 1} + L \right) \right\} } \\
&{} \hspace{15mm} \underline{+ \sqrt{L^2 + 1} - \sqrt{L^2 + a^2}}
\end{align}
$$

と計算できる。

(3)

$a \to +0$ で $\log a \to - \infty$ であり，$\log \left( \sqrt{L^2 + a^2} + L \right)$, $\log \left( \sqrt{L^2 + 1} + L \right)$, $\sqrt{L^2 + 1}$, $\sqrt{L^2 + a^2}$ は正または負の無限大に発散しないため $- L \log a$ の項だけが残り，

$\displaystyle\lim_{a \to +0} \displaystyle\frac{f(a)}{\log a} = \underline{-L}$

となる。